תחומי עליה וירידה של גרף הנגזרת
תיאור האירוע
תרגול הנושא: תחומי עלייה וירידה של פונקציית פולינום.
המורה מציגה את הנושא ומסבירה כיצד מוצאים תחומי עליה ותחומי ירידה של פונקציה. לאחר מכן מציגה את המשימה.
שחר ניגש לפתור את המשימה על הלוח:
\(y=x^3-3x^2+3x+1\)
הנגזרת של הפונקציה היא: \(y’=3x^2-6x+3\) נשרטט את גרף פונקציית הנגזרת לפי סימן המקדם של \(x^2\) ולפי נקודות החיתוך של גרף פונקציית הנגזרת עם ציר ה- \(x\):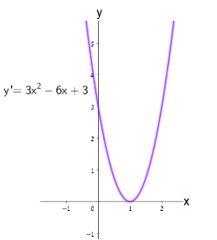
שחר מציב \(y’=0\) ומוצא שנקודת החיתוך של גרף פונקציית הנגזרת עם ציר ה- \(x\) היא \((1,0)\).
מכיוון שהמקדם של \(x^2\) הוא \(3\), אז גרף פונקציית הנגזרת הוא פרבולה בעלת נקודת מינימום, ולכן גרף הנגזרת כולו אי-שלילי. מכאן שהפונקציה עולה לכל \(x\).
מיכל: אני לא מבינה למה אתה אומר שהפונקציה עולה לכל \(x\), כשלפי הסרטוט הפונקציה עולה כאשר \(x>1\) ויורדת כאשר \(x<1\).
המורה: שחר, אתה רוצה לענות למיכל?
שחר: הסקיצה של הפונקציה הריבועית היא של פונקציית הנגזרת, ובקשו שנמצא תחומי עליה וירידה עבור הפונקציה הנתונה. את תחומי עליה וירידה של הפונקציה המקורית מוצאים לפי תחומי החיוביות והשליליות של פונקציית הנגזרת. כיוון שפונקציית הנגזרת היא אי שלילית לכל \(x\) (חיובית או \(0\)) אז הפונקציה המקורית עולה לכל \(x\).
מיכל מתייחסת לתחומי העלייה והירידה של פונקציית הנגזרת במקום לתחומי העלייה והירידה של הפונקציה המקורית. השגיאה של מיכל יכולה לנבוע ממספר סיבות:
- הסקה ויזואלית: מיכל רגילה לראות סקיצה של פונקציה ולא סקיצה של פונקציית הנגזרת. היא מסתמכת על הסרטוט למציאת תחומי העלייה והירידה. מבחינתה, המסקנה של שחר, שהפונקציה עולה לכל \(x\) לא תואמת את הסרטוט.
- השלכה מניסיון על בעיה חדשה: מיכל מבססת את הטענה שלה על הדרך בה למדו למצוא תחומי עליה וירידה של פונקציה ריבועית בכיתה ט’, לפיה מציירים את גרף הפרבולה של הפונקציה הריבועית, וממנה מסיקים את תחומי העלייה והירידה בהתאם לשיעור ה- \(x\) של נקודת הקודקוד.
- מיכל מתקשה לזהות את הקשר שבין התנהגות פונקציה בתחום מסוים לבין סימן הנגזרת שלה בתחום זה, (בזמן ששחר מסיק על התנהגות הפונקציה המקורית מתוך חקר של פונקציית הנגזרת).
המורה רוצה לקדם תרבות של למידת עמיתים בכיתה. היא נמנעת מלתת את ההסבר לפתרון של שחר בעצמה, ומאפשרת לשחר להסביר את עצמו בפני מיכל. בעצם כך, היא מרוויחה גם העמקה נוספת של שחר בפתרון של עצמו, מתוך הצורך לנסח את עצמו ולהסביר אותו למיכל, וגם את חיזוק הביטחון של התלמידים בעובדה שהם יכולים ללמוד זה מזה, ושספר הלימוד או המורה אינם מקור הסמכות והידע הבלעדיים בכיתה.
בדרך זו, המורה מעצימה את התלמיד המשתתף, במקרה זה שחר, ומשקפת לו שהוא בקיא בחומר הנלמד מספיק כדי להסביר אותו לאחרים. בתוך כך, היא גם לוקחת את שחר כדוגמה, כדי לעודד את שאר התלמידים בכיתה לגלות יכולתם ומסוגלות שלהם בלמידה.
- אפשר להסביר באופן מפורש את הדמיון והשוני בין חקירה ומציאת תחומי עליה וירידה בפונקציות ריבועיות באופן אלגברי (כיתה ט’) לחקירת פונקציות (מציאת תחומי עליה וירידה בפולינום ממעלה שלישית ומעלה) בעזרת נגזרת בכיתה י’. הסבר מפורש עושה לתלמידים “סדר בראש” וחלק מהתלמידים זקוקים לו כדי לעבור הלאה לנושאים הבאים.
עד כה, כדי למצוא תחומי עליה וירידה של פונקציה ריבועית, התלמידים סרטטו פרבולה המתאימה לייצוג האלגברי וקבעו את תחומי העלייה והירידה בהתאם לשיעור ה- \(x\) של נקודת הקודקוד. בפונקציות פולינום ממעלה שלישית ומעלה יכולה להיות יותר מנקודת קיצון אחת, או שאין נקודות קיצון כלל. כדי למצוא את תחומי העלייה והירידה בפולינום אפשר לפעול באחת משתי דרכים:
– להציב את ערכי הנקודות החשודות לקיצון בטבלה ולבדוק את סימן הנגזרת בתחומים שבין הנקודות ה”חשודות”, כדי להסיק לגבי עלייה או ירידה של הפונקציה בתחומים אלו.
– במקרה שהנגזרת היא פרבולה (כמו באירוע הזה), ניתן לסרטט את גרף הנגזרת ישירות, מתוך התבוננות בתחומי החיוביות והשליליות (כפי שעשה שחר), וכך לקבוע את תחומי העלייה והירידה של הפונקציה. בדרך זו נדרשת הבנה של הקשר בין חיוביות ושליליות השיפועים לבין עליה וירידה של הפונקציה הנתונה.
בכל אופן, מומלץ לבצע סיכום עם התלמידים יחד. - אפשר לקשור בין הדרכים השונות:
לבקש מתלמיד.ה שפתר.ה את השאלה על ידי טבלה למציאת סוג הקיצון, לבוא ללוח ולשתף בפתרון. מרגע שיונחו שני סוגי הפתרונות הלוח – פתרון באמצעות גרף הנגזרת מול פתרון באמצעות טבלה – יהיה אפשר לקשר באופן מפורש בין סימוני הנגזרת המופיעים בטבלה לבין גרף הפרבולה, ולהראות שכאשר הנגזרת חיובית בטבלה, בתחום זה גרף הנגזרת גם כן חיובי, וכן הלאה. לאחר מכן, אפשר לסרטט את גרף הנגזרת וגרף הפונקציה באותה מערכת צירים, ושוב לדון בקשרים שבין גרף הנגזרת, לטבלה ולגרף הפונקציה המקורית.
תוך כדי חקירה ניתן לשאול:
– איזו פונקציה יורדת כאשר \(x<1\)?
– באיזו פונקציה נדרשנו למצוא תחומי עליה וירידה?
– מהם תחומי החיוביות והשליליות של הפונקציה הריבועית?
– מה הקשר בין פונקציית הנגזרת לבין הפונקציה המקורית?
– מהם תחומי העלייה והירידה של הפונקציה הנתונה?
עברו יחד עם הלומדים על נושאי הלימוד בפרק האנליזה ומצאו יחד מקומות נוספים בהם חקירה של פונקציית הנגזרת מפשטת את חקירת הפונקציה המקורית. למשל, הוכחה שפונקציה עולה/יורדת לכל, חקירת פונקציית מנה וכן הלאה.
המשימה המתמטית
נתונה הפונקציה: \(y=x^3-3x^2+3x+1\).
מצא את תחומי העלייה והירידה בפונקציה זו.


