?Calculating the area of a triangle, or calculating an integral
Type of event: Incorrect mathematics
(Level: Intermediate track (4-unit
Grade: 11th- grade
Topic: Calculus
The mathematical task
(Matriculation Questionnaire 841, Winter 2011, special test date for combat soldiers)
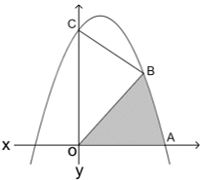
In the illustration is a parabola, \(y=-x^2+2x+8\).
A and C are the points at which the function intersects the axes.
I). Find the coordinates of points A and C.
II). B is a point on the graph in the first quadrant such that the area of the triangle OBC is 12 \(cm^2\) (O is the origin). Find the coordinates of point B.
III). Find the area between the graph of the function, the line OB, and the x-axis.
Description of the event
This lesson was a review in preparation for the Bagrut (Matriculation) exams (solving Part C of the task). Students were asked to solve the task independently.
Danny: I found that the coordinates of point A are \( (4,0)\) and the coordinates of point B are \((3,5) \). I calculated the area using the altitude of the triangle (the \(y \)-value of point B) multiplied by the length of its side \( (AO=4)\), divided by two. Therefore, the area of the triangle is \( \frac{4\cdot5}{2} \), that is, 10 \( cm^2\).
The teacher presents Danny’s solution to the class and asks: What do you think of this solution? What’s your opinion? Explain your answer.
A debate begins over whether or not the solution is correct, during which the teacher explains that the calculation is imprecise because the parabola is a curved line and the side of a triangle is a segment of a straight line.
Danny calculated the area of the triangle OBA as if it were the requested area.
1. Mistaken visualization: The illustration is misleading – the segment of the parabola in question looks like a line segment, not like a curve that is part of a parabola. Danny, relying on the illustration, concluded incorrectly that the area he needed to calculate was, essentially, a triangle.
2. Inattention and failure to check the answer: Danny did not pay attention to the information given in the question. He ignored the fact that the graph was the graph of a quadratic function, and that the segment AB was part of a parabola. If he had used the data given in the question, he would have calculated the area using an integral.
- The teacher chose to bring Danny’s mistake to the attention of the entire class. It was important to him that everyone make note of the mistake, in order to prevent them from making the same mistake on the upcoming test.
- The teacher wanted the students to participate in explaining the source of the mistake. It was important to him that the students review the concept of using a definite integral to calculate area. He wanted the students to notice for themselves that the segment between A and B was a segment of a parabola, and that the area under the curve should not be calculated as if it was the area of a triangle.
- The teacher wanted to make students aware of the importance of checking their answers. To remind students that when solving an exercise, they need to read the givens carefully, and at the end, they need to return to the given data and check that they made correct use of it and that they solved the problem they were asked to solve.
Use of the GeoGebra program: Beyond what the teacher did, there could have been discussion about calculating a definite integral in the following ways:
1. Reviewing the meaning of calculating a definite integral using the integral (link).
2. Discussing the differences in the results of the two calculations – the calculation using the formula for the area of a triangle, versus the calculation using a definite integral – and illustrating the difference using the applet.
The teacher can use the applet to move point B, and, together with the students, examine how the difference between the formula for the area of a triangle and the calculation of area using an integral grows and shrinks, depending on point B (the teacher could let the students experiment, and explain the results).
Below is an illustration of the results when using the applet: the point is moved, and the area changes accordingly. The difference between the area in the question and the area of the triangle changes each time the point moves. (The smallest difference occurs when the x-value of B is 3, as given in the question.)
In purple – the area that was calculated using the formula for area of a triangle.
In pink – the area students were asked to find, calculated using a definite integral.



Moreover, the teacher could examine, together with the students, the error involved when using a Reimann integral with rectangles, and compare it to the error obtained when estimating using other shapes, such as trapezoids (link).
What might be the benefits and/or drawbacks of various methods of estimation? A discussion such as this can begin with the given problem, via inductive reasoning using rectangles or trapezoids, and from there, could be expanded to an attempt to draw general conclusions about mathematical rules.
Hold a discussion about the event. Use the questions:
a. What was the event? Why, in your opinion, was this event a critical event?
b. What did the student say/do?
c. What do you think was the reason for the student’s error?
d. What could a teacher do in this situation?
e. Would it be worthwhile for the teacher to review the significance of mathematical objects, or should he make do with correcting the mistake? What are the benefits and drawbacks of reviewing the meaning of an integral, and what are the benefits and drawbacks of simply correcting the mistake?


