Extending Thales’ theorem
Type of event: Extending
(Level: High track (5-unit
Grade: 10th- grade
Topic: Geometry
The mathematical task
Formulate the converse to Thales’ theorem:
If a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio
If DE∥BC, then \( \frac{AD}{AB}=\frac{AE}{AC} \).
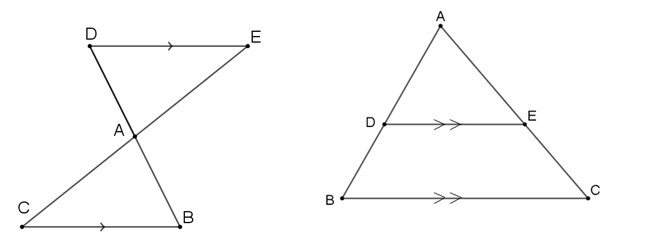
Description of the event
The teacher began the lesson by writing the theorem on the board, as a reminder of the previous lesson (the students were asked to formulate the converse of the theorem).
Maayan: Okay, could we maybe say that if the ratio \( \frac{AD}{AB}=\frac{DE}{BC} \) holds true then the lines are parallel?
Teacher: Maayan’s question could be formulated as a mathematical argument. “If \( \frac{AD}{AB}=\frac{DE}{BC} \), then DE∥BC.” How can we check whether the argument is true? What mathematical tools do we have? [Waits a few seconds]. We need to prove it. Essentially, we will use the argument as a “given” in the question and see if we manage to get to the conclusion that DE∥BC.
Do you have any ideas about how we could do that? I’d like you to start working on it in pairs. I’ll just remind you that to prove that an argument is true, you have to show that it is true in the general case, while to disprove an argument, a single counter-example is enough. The students work in pairs. Ten minutes before the lesson ends, a whole class discussion is held where students present their findings.
Noya: [Goes to the board, draws, and explains] I think the argument can be disproven like this: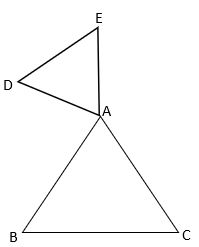
In this case, if for example, the triangles are similar, then the ratio will be \( \frac{AD}{AB}=\frac{DE}{BC} \), but the lines DE and BC are not parallel!
Teacher: Very nice! Very nice idea! [To the class] What do you think of Noya’s explanation?
Students: Excellent!
Teacher: I also think this is a great idea, there’s just one small problem here. Who can tell me what the problem is?
Yarden: Maybe it doesn’t have to do with the converse of Thales’ theorem? I don’t really know, it’s just that that’s the topic of the lesson…
Teacher: You’re on the right track, Yarden. Maayan’s argument is a variation of the converse of Thales’ theorem. The converse of Thales’ theorem talks about two straight lines that intersect the legs of an angle. That is, either of the two following situations: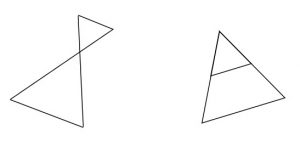
Teacher: Any other ideas?
Lotan: I had a thought. Can I come and explain it?
Teacher: Of course, come on up.
[Lotan approaches the board, and draws]
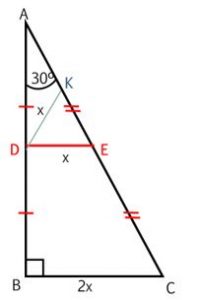
Lotan: The triangle ABC is a 30°,60°,90° triangle. We add the midline DE to the triangle and mark it as \(x\). If DE equals \(x\), then BC equals \(2x\) . BC is the side opposite the 30-degree angle in a right triangle, so it is half the length of the hypotenuse. The hypotenuse is \(4x\), and AE and CE are equal, \(2x\) each. By construction, the triangle ADE is similar to the triangle ABC. From the vertex D we draw a medial line to the hypotenuse AE, and mark it as DK. In a right triangle the median line to the hypotenuse is half the length of the hypotenuse, so DK is also equal to \(x\). So we got:
\( \frac{AD}{AB}=\frac{DK}{BC}=\frac{1}{2} \)
But DK and BC are not parallel lines!
- Maayan’s proposal was not the converse of the Thales’ theorem, but rather a variation of it. She tried to expand the converse of the theorem beyond the wording that reverses “if” and “then,” which appeared to her to be trivial, and worded it as if it were a proportionate trio, based on her previous knowledge regarding similarity and proportionality of triangles.
She thought that when two pairs of sides have the same ratio, then the same proportion holds between the sides of the third pair. Thus, to her, equal ratios between two pairs of sides are enough to show that the sides are parallel. Maayan’s mistake stemmed from the fact that she overlooked the fact that the segments are on the sides of the angle.
- Noya sees the difference between expanding on the converse of Thales’ theorem, and a proportionate trio of sides. She uses her knowledge of similar triangles to disprove Maayan’s argument: she assumes that two triangles are similar, to show that the proportional relationship between two pairs of sides does not mean the third pair is necessarily parallel. However, she ignores a “hidden” given at the base of Thales’ theorem, which is a situation in which two straight lines intersect the sides of an angle.
- Lotan bases her solution on a special triangle – a right triangle with a 30-degree angle – which has a wide array of properties. In addition, her idea adopts part of Noya’s idea – shifting the shape. Lotan shifts the side of the inner triangle, rotating it, and this creates a counter-example sufficient to disprove the argument.
- The teacher identified the incident as an opportunity to conduct an interesting investigation of an argument that appears to be logical, but may not be true. She decided to deviate from the lesson plan and allow students to work on proving the argument.
- The teacher wants to emphasize the power of proofing as a tool to check whether an argument is correct. Each “theorem” that the students prove is an argument that can be tested. In general, students test the arguments in textbooks which they are asked to examine, which are generally true. Here, they have an opportunity to examine an argument that may or may not be true – an argument that arose due to students’ natural curiosity. Investigating an unfamiliar argument can inspire the class to action, and encourage them to use all of the geometric tools at their disposal.
- The idea at the base of disproving the argument is that there is a situation that is preserved – two straight lines that cut the legs of an angle at equal proportions. The students could be asked to think of other inverse theorems for which it is important to state that a certain situation must be maintained in both directions. For example, the angle bisector theorem converse – for the theorem: If \( \frac{CD}{BD}=\frac{AC}{AB} \), then \( \measuredangle CAD=\measuredangle BAD \) to be true, it is necessary to state that the theorem holds true for a situation in which a segment connects the vertex of a triangle to the opposite side, as illustrated:
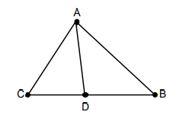
- An activity of this type trains the students to identify the givens that constitute the “preserved situation” (a triangle in which a segment connects the vertex to the opposite side), even if it is not explicitly written. This way, the switch to the converse theorem will be made correctly, without mistaken assumptions along the way.
- Suggestion for working on geometry task: Ask the students to create a drawing to illustrate Maayan’s argument, and then to attempt to prove based on the “rules of the game” in the illustration. A discussion such as this may encourage more students to get involved, including those who feel like they can’t address the argument without an illustration.
After agreeing on an illustration relevant to the givens in the problem, students can be asked to list all of the information that stems from the givens in the task and that they believe is relevant, and finally, students can prove the argument in the task independently. In an activity of this type, there is both a review of many geometric properties and a discussion about the relevance of each property to solving.
- Present Maayan’s argument to the trainees. Ask for their opinions – is Maayan’s argument true? Ask them to prove or disprove the argument. Present their proofs to the class, just as happened in the classroom in the event. If they do not reach the correct conclusion, the two counterexamples – Noya’s and Lotan’s – can be presented, and the trainer can ask what the trainees think of each of the examples, and which of them is a suitable counterexample that disproves the claim.
- The idea at the base of the counterexample that disproves the argument is that there is a situation that is preserved – two lines that apportion proportional segments on the legs of an angle. The trainer can ask the trainees to read the article in the next section, and to discuss additional situations in which looking at what is preserved in various situations matching the description in the task, and what changes, affects how the students understand and approach the task.


