Why does Yinon think that the maximum area is found when the width and length are equal?
1. Trial and error based on intuition: Yinon tries to get the maximum area for the plot of land by checking pairs of numbers, and finds that the area is maximum when the length and width are equal (the rectangle is a square).
2. Using a mistaken calculation:
As proof, Yinon uses a pair of numbers for which the argument is true:
\({25}\cdot27<{26}\cdot26 \)
This result could be obtained using either of the two calculations.
The first:
\(        25\cdot27=25\cdot(26+1)=25\cdot26+25\cdot1 \)
\(        26\cdot26=26\cdot(25+1)=25\cdot26+26\cdot1 \)
The product in the first row is smaller than the product in the second row, therefore the left side is smaller than the right side.
The second:
Using the formula for the difference between squares:
\(        25\cdot27=(26-1)(26+1)=26^2-1^2<26\cdot26 \)

Yinon’s solution also reflects his experience (from 9th grade) in determining the sign of inequality between algebraic expressions with parameters. Thus, for: \(       a,b\neq 0 \) \(       (a-b)(a+b)<a\cdot a \) because \(       (a-b)(a+b)=a^2-b^2 \) and \(      a^2-b^2<a^2 \). That is, in a case like this the maximum product is obtained when the factors are equal.
3. Relying on a single case: When formulating his argument, Yinon uses a specific example in place of proof. He believes that if the argument is true for one example (or more) of a pair of numbers, it must be true in all cases.
4. Relying on past experience: Yinon remembers, from previous math activities in 9th or 10th grade, that the maximum area is obtained when a polygon is regular (activities discussing shapes with equal perimeters and different areas, or equal areas and different perimeters, in which students draw conclusions about the perimeter or area).

1. Yinon is suggesting a solution that matches a specific instance of a square (or regular polygons), for which maximum area is obtained. In this case, the teacher chooses to discuss Yinon’s suggestion only after solving the question the traditional way, by building a target function, which is an early stage in the process of solving extremum problems (before taking the derivative and finding extrema).
If the topic of problems involving extrema was not yet learned in class, the teacher’s decision to solve in this way was aimed at preventing future confusion, particularly when solving other questions in the same topic (in the future, students will learn the other procedures, and will become familiar with the many other types of problems involving extrema).
2. The teacher did mention Yinon’s solution because he recognized it as resulting from original thinking, which he wanted to encourage. He did so through a class investigation of Yinon’s solution method, which allowed him to emphasize to the class the importance of independent thought and creativity in solving tasks. This indicated to the rest of the students that thoughts like these can be shared in class, and will receive a favorable response.
3. The teacher asks Yinon to prove his argument for additional cases, beyond the example he gave. He does so in order to stand on principle: a specific example is not sufficient; only formal proofs are accepted.

This event emphasizes the importance of talking about the need for a formal proof, and the fact that one example, or even many examples, are not enough to prove that an argument is correct.
This can be done in class by presenting a different (incorrect) argument, which is true in a certain case, and then bringing a counter-example or asking the students to find a counter-example. For instance, an argument that is true for a specific case could be: if the diagonals of a quadrilateral are equal, the quadrilateral is a rectangle. An illustration can also be used: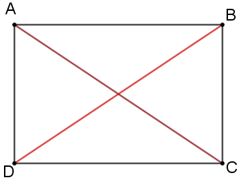

 
The argument is true for the quadrilateral in the illustration: the diagonals are equal, and the quadrilateral is a rectangle. This specific example cannot be generalized and does not prove the argument that every quadrilateral with equal diagonals is a rectangle.
As a counter-example, we present an isosceles trapezoid, which has equal diagonals but is not a rectangle. Thus, we see that not every quadrilateral with equal diagonals is a rectangle.

1. Split the trainees into groups, and have them try to prove the student’s argument by checking different numbers. This, without having read the teacher’s response first.
2. Ask the trainees to give an example of an incorrect argument and a counterexample that they used in their classroom when they needed to illustrate the importance of a formal proof.
3. Discuss with the trainees: in the context of this event, at what stage would they discuss the student’s solution? Discuss the benefits and drawbacks of each suggestion.
4. Discuss the benefits and drawbacks of using the task that appears in the event when introducing the subject of problems involving extrema. Emphasize the question: what are the different types of learning that this task invites?

For example: methods of presenting a parabolic equation, and finding the vertex of a parabola in different forms. In general, solving a task of this type in class allows for expanding students’ mathematical knowledge. In this case, for example, Yinon’s answer provided an opportunity for a general discussion regarding the connection between regular polygons and maximum area (when the perimeter is given). The drawback of using this task when beginning the topic is that it may be solved quickly (as happened in this event), and the need for a method for solving problems involving extrema can get lost along the way. In order to overcome this difficulty, it is better to bring a task with a third-degree equation, for which finding the extrema is less intuitive.