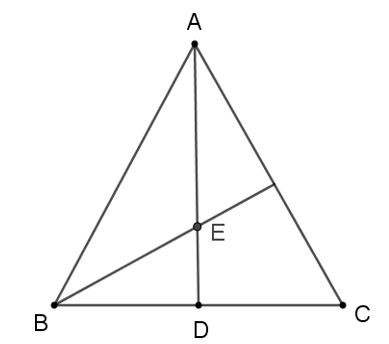
האם חוצה זווית במשולש הוא גם תיכון?

1. הכללת יתר במילה “מפגש”: התלמידים מבלבלים את משמעות המילה “מפגש” וטועים לחשוב כי מדובר בנקודת מפגש לתיכונים (ברבים).
2. השלכת תכונות בין קטעים שונים: התלמידים משליכים מתכונה של הקטע AD, שהוא תיכון על הקטע הממשיך את BE איננו תיכון.
3. משמעות אובדת במהלך פתרון: שימוש שגור במשפט “במשולש שווה שוקיים, חוצה הזווית הוא גם תיכון” מביא את יואל ושני לאבד חלקים מהמשפט בדרך. במקרה זה, לא התייחסו התלמידים לחלק במשפט “חוצה זווית הראש”.
4. ויזואליציה מטעה: המשולש בסרטוט נראה כמו משולש שווה צלעות.
   התלמידים תופסים את המשולש הנתון כשווה צלעות, מבלי להוכיח את נכונות הטענה.
5. השלמה אוטומטית: המשפט על מפגש התיכונים במשולש הוא המשפט בעל השימוש הרב יותר בתוך שיעורי הגיאומטריה מבין ארבעת המשפטים העוסקים במפגש קטעים מיוחדים במשולש. קריאה מהירה ולא זהירה את המילה “מפגש” בנתונים הביאה את התלמידים להשלים בראש את המשפט שהם מכירים על מפגש תיכונים.

1. בהצגת הפתרון של יואל, המורה מסב את תשומת לב התלמידים לקריאה מחודשת של הנתונים, מתוך נקודת הנחה שהטעות נובעת מחוסר תשומת לב בקריאתם. בהצגת חוזרת של השגיאה אצל שני, המורה מסיק שיש כאן מצב לטעות מסוג אחר של הרחבת יתר – השלכת התכונות של קטע אחד על קטע שני, ולכן הוא מחדד את הנתון על המפגש.
2. המורה מנחה את התלמידים לקרוא שוב את נתוני השאלה: הנקודה E היא לא נקודת מפגש התיכונים, אלא נקודת מפגש חוצי הזווית, ורק אחר כך מדייק את הטעות. הוא מעוניין לתת לתלמידים לגלות את השגיאה בכוחות עצמם תחילה, לפני שיתקן אותם.

1. אפשר לשאול שאלות מנחות כדי להתחקות אחר מקור הטעות. השאלות המנחות נועדות להחזיר את התלמיד לפרט את התשובה שלו, כך שיהיה אפשר לבחון יחד כל שלב בדרך, עד שהתלמיד מוצא את הטעות בעצמו. למשל:
     – לפי מה שאתה אומר, הקטע AD תיכון, מכיוון שהוא חוצה זווית הראש במשולש שווה שוקיים. האם מדובר כאן במפגש תיכונים? (ברבים)
     – האם גם חוצה הזווית שיוצא מקודקוד B הוא תיכון?
     – כמה תיכונים צריכים להיפגש במשולש, על מנת להסיק כי נקודת המפגש היא אכן נקודת מפגש התיכונים במשולש?
2. אפשר לתת דוגמה נוספת. במקרה זה, למשל, אפשר לתת דוגמה של משולש אחר בו נפגשים שני חוצי זוויות, ורק אחד מחוצי הזוויות הוא גם תיכון. לצורך העניין, חשוב לסרטט משולש שברור מבחינה ויזואלית שהוא אינו שווה צלעות.
3. אפשר להשתמש בבניות הייעודיות של תיכון, חוצה זווית, אנך אמצעי באמצעות השימוש ביישומון- GeoGebra, או לחילופין, לבנות את הקטעים בעזרת “סרגל ומחוגה” דיגיטליים. לתת כמשימה לשיעורי בית, או בעבודת כיתה. לדוגמה:
     – בנו את המשולש ABC∆ ב- GeoGebra, באופן הבא:
     – שרטטו את הבסיס BC.
     – בנו את האנך האמצעי לבסיס BC.
     – סמנו נקודה כלשהי על האנך האמצעי (לא נקודת החיתוך עם הבסיס, כדי שייווצר משולש).
     – חברו את הנקודה שסימנתם בסעיף הקודם עם קודקודי הבסיס BC.
     – קיבלתם משולש שווה שוקיים, בו האנך האמצעי הוא חוצה זווית A – הסבירו מדוע.
   נשנה את המשולש על ידי גרירת קודקוד הראש, כדי להיווכח שחוצה הזווית שיוצא מנקודה B אינו בהכרח תיכון. נעשה זאת בעזרת השלבים הבאים:
     – בניית חוצה זווית היוצא מקודקוד B.
     – מציאת נקודת האמצע של השוק מול קודקוד B (כלומר צלע AC).
     – חיבור קודקוד עם נקודת אמצע צלע AC.
     – מתוך בניה זו קיבלנו את התיכון ל- AC. על ידי גרירת קודקוד הראש של המשולש שבנינו ניתן לראות כי חוצה הזווית שיוצא מקודקוד B אינו בהכרח התיכון לצלע.
   אפשר להמשיך לחקור את הבנייה ב GeoGebra ולבדוק באיזה מקרה חוצה הזווית היוצא מנקודה B יהיה גם תיכון (כשהמשולש הוא שווה צלעות). היתרון בשימוש ביישומון בפעילות הוא האפשרות לחקר חוויתי. בניות ב- GeoGebra יכולות להמחיש בכל מצב את ההשפעה של שינוי מסוים בנתוני השאלה על נכונות הטענה המתמטית.

פעילות א’
מטרות הפעילות:

1. הלומדים יכירו מצבים של הסקת מסקנות שגויה ויתרגלו מיומנויות של בדיקת נכונות של טענה.
2. הלומדים יפנימו את החשיבות של התחקות אחר מקור הטעות, וגם את ההבדלים בהשלכות של טעויות מסוגים שונים ויכירו דרכים כיצד למנף את הטעות ללמידה.

מהלך הפעילות:

• חלקו ללומדים את החלק הראשון של תיאור האירוע (עד לטענת התלמיד). בקשו מהם לבדוק את נכונות הטענה. בקשו מהם לזהות ולסמן בטקסט מה הרגע הקריטי בשיעור, לדעתם, ולנמק את בחירתם.
• ערכו דיון במליאה על טענת התלמיד באירוע, ועל השלכות שיש להסקת מסקנות שגויה על פתרונות באופן כללי.
• חלקו ללומדים את שאר האירוע הכתוב (מהרגע שבו המורה מפנה את התלמיד להסתכל בנתוני השאלה ועד סופו). נהלו דיון על מה שקראו:
  • מה לדעתכם מקור הטעות של התלמיד?
  • מה הוביל את המורה לבקש מהתלמיד לקרוא שוב את השאלה?
  • מה גרם למורה לחדד בעצמו את הטעות בטענה של התלמיד?
  • מה ההבדל בין סוגי הטעויות – טעות נגררת הנובעת מחוסר תשומת לב בקריאת נתוני השאלה (החלפת המילה “חוצי זווית” במילה “תיכונים”) מול טעות של הכללת יתר והשמטת מילה במשפט “במשולש שווה שוקיים, חוצה זווית הראש הוא גם תיכון”.
    מה המשמעות של כל אחת מהטעויות?

פעילות ב’ :
מטרות הפעילות:

1. הלומדים יבינו את הבעייתיות בניסוח משפט שחסרה בו מילה, אשר בחסרונה ניתן להבין את המשפט בצורה שונה ולהגיע למסקנות שגויות וירכשו מיומנות של הבחנה בחסר זה.
2. הלומדים יתנסו בהסתכלות מזווית מבטם של התלמידים ויתחקו אחר דרך חשיבתם, כדי לאתר טעויות ותפיסות שגויות אצלם. ניסיון זה מטרתו לעורר מודעות לחשיבות של ניסוח תקין ומדויק של המשפטים, וכן לתת ללומדים כלים כמורים לעתיד, כיצד יוכלו לעזור בהמשך להסיר תפיסות שגויות אצל תלמידים.

מהלך הפעילות:

• חלקו ללומדים את האירוע במלואו כטקסט כתוב.
• בקשו מהם לסמן בטקסט את הקטע המשמעותי בו לדעתם.
  בערכו דיון סביב טענת התלמיד המוצגת בטקסט. הדיון יכול להכיל את השאלות הבאות:
• אילו מילים חשובות נשמטו במשפטים אותם מצטט התלמיד?
• אילו טעויות יכולות להתרחש כתוצאה מהשמטת מילים מסוימות במשפטים בגאומטריה?
• בקשו מהלומדים לתת דוגמאות משלהם למשפטים נוספים בהם מילה חסרה יכולה לגרור טעות מהותית.
  בקשו מהם לנמק ולהסביר, היכן בדיוק יכולה ליפול הטעות ומה ההשלכות.

דוד, ח’. (2007). שימוש בשגיאות של תלמידים כמנוף לשיפור הלמידה ולהעמקת הידע המתמטי. על”ה, 37. 81-93.

רייז, ר’ . (2007). טעויות של תלמידים כמנוף להוראה. קש”ר חם.

טעויות של תלמידים כמנוף להוראה