הוצאת שורש מסדר זוגי של משתנה
תיאור האירוע
תרגול במליאה: מציאת אסימפטוטה אופקית לפונקציית מנה עם שורש במכנה.
המורה מפרטת את שלבי הפתרון על הלוח:
\(\displaystyle \lim_{x \to \infty} \frac{2x+1}{\sqrt[4]{81x^4+9}}=\displaystyle\lim_{x \to \infty}\frac{2x+1}{\sqrt[4]{x^4 (81+\frac{9}{x^4})}}=\)
\(\displaystyle\lim_{x \to \infty}\frac {\frac{2x+1}{x}}{\frac{\sqrt[4]{x^4 (81+\frac{9}{x^4})}}{x}}=\displaystyle\lim_{x \to \infty}\frac{2+\frac{1}{x}}{\frac{\sqrt[4]{x^4 (81+\frac{9}{x^4})}}{x}}=\displaystyle\lim_{x \to \infty}\frac{2}{\frac{\sqrt[4]{x^4 (81)}}{x}}\)
המורה: כאשר נוציא שורש רביעי מהביטוי במכנה שנמצא בתוך השורש, מה נקבל?
תלמידים: נבצע פעולת שורש רביעי גם על המספר 81 וגם על הנעלם \(x^4\) ונקבל \(\sqrt [4]{81 x^4}=3x\).
המורה: לא מדויק. התוצאה צריכה להיות \(3|x|\) ואז \(\displaystyle\lim_{x \to \infty}\frac{2}{\frac{\sqrt[4]{x^4 (81)}}{x}}=\frac{2}{\frac{3|x|}{x}}=\frac{2}{3}\). כלומר, עבור \(x\) שואף לאינסוף האסימפטוטה האופקית היא \(\frac{2}{3}\).
תלמידים: למה? זה לא ברור למה צריך כאן ערך מוחלט, ולמה התשובה \(3x\) לא מדויקת?
המורה: אמנם קיבלנו את אותה אסימפטוטה אופקית שהיינו מקבלים אם לא היינו מוסיפים ערך מוחלט, אך עבור איקס השואף למינוס אינסוף, האסימפטוטה האופקית היא \(-\frac{2}{3}\) ולכן זה לא מדויק. התוצאה במקרה זה מושפעת מן הדיוק של הוספת סימן ערך מוחלט.
בוא ננסה להבין למה התשובה כאן היא \(3|x|\).
למה שווה\(\sqrt{4}\)?
תלמידים: 2.
המורה: יפה. ולמה שווה \(\sqrt{x^2}\)?
תלמידים: ל- \(x\).
מורה: בואו נבדוק. קודם כל, שאלה אחרת מהו הפתרון של \(x^2=4\)?
תלמידים: יש שני פתרונות: \(x_{1}=2 \space\space;\space\space x_{2}=-2\)
המורה: טוב, עכשיו נסביר למה בהוצאת השורש ב- \(\sqrt{4}\) וב- \(\sqrt{x^2}\) זה לא עובד אותו הדבר.
בפתרון משוואה ממעלה שניה רוצים לבטל את החזקה על ידי פעולה הפוכה, כלומר על ידי הוצאת שורש, ככה:
\(x^2=4 \space \rightarrow \space x =\pm \sqrt{4} \space \rightarrow \space x_{1,2}= \pm 2\)
לעומת זאת, פעולת השורש נותנת תוצאה חיובית. למשל \(\sqrt{4}=2 \space\space; \space\space \sqrt{9}=3\)
שלא כמו העלאה בריבוע \(x^2=25\) שהפתרונות שלה הם: \(x_{1}=5\space\space; \space\space x_{2}=-5\).
זה קורה בגלל שבפתרון משוואה ריבועית יכולה להתקבל גם תוצאה שלילית. בעצם, שני הפתרונות מקיימים את המשוואה: \((5)^2=25\) וגם \((-5)^2=25\). כשאנחנו שואלים: איזה מספר בריבוע יהיה שווה \(25\), התשובה היא \(5\) וגם \((-5)\).
כאשר מדובר על משתנה מתחת לסימן השורש מתקיים:
\(\sqrt{x^2} = \left\{ \begin{array}{cc}
x & \hspace{1mm} x>0 \\
& \hspace{1mm} \\
-x & \hspace{1mm} x<0 \\
\end{array} \right. \)
כלומר: \(\sqrt{x^2}=|x|\)
במשימה אחרת שפתרו בהמשך השיעור המכנה היה מסדר אי-זוגי.
תלמידים: למה כאן את לא משתמשת בסימון של ערך מוחלט?
המורה: אנחנו לא משתמשים בסימן של ערך מוחלט כשאנחנו מוציאים משתנה משורש מסדר אי-זוגי. משום שבתוך שורש מסדר אי- זוגי יכול להופיע ביטוי שלילי, ובפעולת הוצאת שורש אי זוגי מביטוי שלילי מתקבל ביטוי שלילי.
למשל, נפתור \(\sqrt[3]{-8}=-2\), בגלל ש \(-2\cdot-2\cdot-2=-8\). וכנשאל: איזה מספר כשמכפילים אותו בעצמו שלוש פעמים מקבלים 8-? התשובה תהיה 2-.
- התלמידים לא מבינים למה התוצאה \(3x\) לא מדויקת. הם לא משערים שהביטוי \(3x\) יכול להיות גם שלילי.
- במשימה זו התלמידים נדרשים למצוא את האסימפטוטה האופקית, כאשר \(x\) שואף לאינסוף ולא למינוס אינסוף. לכן הם לא כוללים את האפשרות שהנעלם יכול לקבל מספרים שליליים.
- התלמידים רגילים שבפתרון משוואות מתייחסים גם לתוצאות שליליות. (הם נותנים למורה את התשובות: 2 ו- 2- כשהם מתבקשים לפתור את \(x^2=4\) נראה שהם מתייחסים להוצאת השורש הרביעי כאל משוואה, ולא כאל פעולה שיש לוודא שהתוצאה שלה תהיה החיובית בלבד.
- במשימה הבאה שבה היה שורש מסדר אי-זוגי, היו תלמידים שסברו כי בדומה למשימה הקודמת, גם כאן יש לכתוב ערך מוחלט. טעות זו יכולה לנבוע משתי סיבות:
– הם מתייחסים להסבר של המורה כאל הסבר כללי (כמעין נוסחה של “כך עושים”), וחושבים שגם כאן צריך לכתוב ערך מוחלט, שהרי גם כאן מוציאים שורש. הם לא מבינים כי השימוש בסימן הערך המוחלט במשימה הקודמת נובע מהוצאת שורש זוגי, שעבורו יכול להתקבל פתרון חיובי ופתרון שלילי.
– הם לא רואים ולא שמים לב שמדובר כאן על שורש מסדר אי- זוגי. למעשה, הם לא מבחינים בין המקרים.
- המורה רוצה להבנות באופן הדרגתי את הצורך בשימוש בסימן הערך המוחלט; כשהיא מזהה את הקושי של התלמידים במשימה הראשונה, היא עוצרת את התהליך כדי לשאול שאלות מכוונות תוך שימוש בתרגילים פשוטים.
בהתייחס לקושי שזיהתה, היא בוחרת לעשות שימוש בדוגמה של פתרון משוואה ריבועית אל מול שורש כפעולה, וכך היא נותנת מענה מדויק לפי הצורך של התלמידים. - במשימה השנייה (שבה היה שורש מסדר אי- זוגי), המורה שמה לב שיש בלבול בקרב התלמידים, ובוחרת להתייחס לבלבול משני כיוונים:
– כשהיא אומרת ש”לא משתמשים בסימן של ערך מוחלט כדי להוציא משתנה משורש מסדר אי-זוגי” היא מתייחסת לתלמידים שטעו בגלל תפיסה חסרה של הפרטים מבחינה ויזואלית.
– כשהיא מוסיפה להסבר דוגמה של הוצאת שורש אי זוגי ממספר שלילי (כדי להראות שבכך מתקבלת אך ורק תוצאה שלילית), היא עושה זאת עבור תלמידים שהבלבול שלהם נובע מחוסר הבנה. ההסבר הזה מיועד לעזור להם להבחין בין המקרים: פעולה של הוצאת שורש מסדר זוגי לבין פעולת הוצאת שורש מסדר אי- זוגי.
א. אפשר להסביר בדרך אחרת, שההגדרה של המושג “שורש” קובעת כי פעולת השורש (מסדר זוגי) נותנת תוצאה חיובית בלבד. כדי להסביר מדוע בפתרון משוואה ריבועית יכולה להתקבל תוצאה שלילית אפשר להציג את התרגיל הבא:
נתונה המשוואה \(x^2=4\)
נוציא שורש משני אגפי המשוואה \(\sqrt{x^2}=\sqrt{4}\). משום ש \(\sqrt{4}=2\) וכן \(\sqrt{x^2}=|x|\), לכן המשוואה הנ”ל שקולה למשוואה: \(|x|=2\).
בשל סימן הערך המוחלט נקבל שני פתרונות: \(x_{1,2}=\pm{2}\).
ב. שימוש בתוכנת GeoGebra:
נגדיר את הביטוי במכנה כפונקציה חדשה \(y=\sqrt[4]{81x^4+9}\) ונשאל את התלמידים: מה המשמעות הגרפית לכך שהפונקציה החדשה \(y\) יכולה לקבל גם ערכים שליליים?
אחרי שמציירים את הפונקציה ביישומון, אפשר לשאול: היכן נמצא גרף הפונקציה? באילו רביעים? מה המשמעות לכך?
הגרף המתקבל: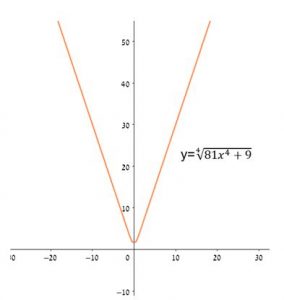 
אפשר לראות שהגרף נמצא ברביעים הראשון והשני. כלומר, ערכי ה-\(y\) בפונקציה זו הם חיוביים, ולכן התשובה המתקבלת מפעולת הוצאת השורש היא \(3|x|\) ולא \(3x\).
הגרף כאן מתאים לסרטוט הפונקציה עם הערך המוחלט \(y=-3|x|\) , ולא לישר \(y=3x\).
בטקסט המקורי יש מינוס לפני פונקציית הערך המוחלט. האם זו לא טעות?
ג. שאלות מכוונות והסבר על דרך השלילה:
אפשר להתבונן יחד בפונקציית שורש מסדר זוגי הפשוטה ביותר: \(y=\sqrt{x}\). ואז אפשר לשאול – אם, נניח, הביטוי \(\sqrt{4}\) שווה \(2\) וגם שווה \(-2\), מה משמעות הדבר מבחינת הנקודות על הגרף?
התלמידים יכולים לראות שעבור \(x=4\) מתקבלים שני ערכי \(y\) שונים. כלומר, היו מתקבלות הנקודות \((4,2)\space,\space(4,-2)\) על אותו הגרף.
ואז אפשר לשאול: אם היינו מגדירים כך את פעולת השורש עבור כל ערכי ה- x, כיצד הגרף היה נראה? ולבקש מהם לצייר .
הגרף שמתקבל: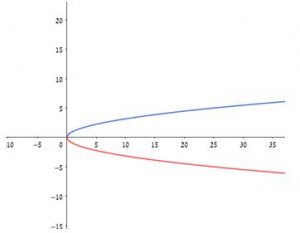 
גרף זה אינו מייצג פונקציה, כי פונקציה מוגדרת כך שעבור כל שיעור \(x\) מתאים שיעור \(y\) אחד בלבד (לא יכולים להתקבל שני ערכי \(y\) שונים עבור ערך \(x\) אחד, כמו למעלה).
הגרף המתאים הוא זה:
זוהי סיבה נוספת למה לא ניתן להגדיר את פעולת השורש כפעולה בה מתקבלות שתי תוצאות שונות עבור שיעור x אחד.
היתרון באסטרטגיה זו, היא המחשה בדרך ויזואלית את הבעייתיות בהגדרת פעולת השורש. המחשה כזאת תחדד את ההבנה בצורה ברורה ומהירה.
פעילות בנושא ההבדל בין פתרון משוואה לפעולה בתוכנית הלימודים:
- הפנו את הלומדים לספריה (או לגוגל) לחפש הגדרה לפעולה מתמטית. דונו במליאה במשמעות של פעולה מתמטית.
- בקשו מהלומדים להתחלק לקבוצות ולהכין פעילות לתלמידים שמטרתה להסביר את ההבדל בין פעולה מתמטית לבין משוואה. הפעילות צריכה להתאים לנושא מתמטי מסוים בו תלמידים עלולים להיתקל בקושי.
- הציגו את התוצרים במליאה.
- לסיכום אפשר לדון איך הקושי בהגדרת הפעולה המתמטית עולה בכל פעם שמתייחסים להוצאת שורש כאל פעולה, ולא כאל משוואה. מדוע לתלמידים קל יותר (ברוב המקרים) להתמודד עם משוואה?
המשימה המתמטית
(חלק ממשימת חקירה מרובה סעיפים)
נתונה הפונקציה: \(f(x)=\frac{2x+1}{\sqrt[4]{81x^4+9}}\)
האם יש לפונקציה זו אסימפטוטה אופקית כאשר \(x\) שואף לאינסוף?