הנחה שגויה בהבעת שטח המחומש באמצעות x
תיאור האירוע
התלמידים פותרים את השאלה בעבודה עצמית. לאחר מכן המורה מרכזת את תשומת ליבם במליאה ומבקשת מהתלמידים לשתף בפתרונות שלהם.
חגית: אפשר לחשב את שטח המחומש הצבוע בסגול כשטח הריבוע הגדול פחות שטחי שני המשולשים הלבנים:
\( S_{ECDAB}=S_{BEFG}-S_{CDF}-S_{ADG}= \)
\( 16^2-\frac{x\cdot{2x}}{2}- \frac{(16-x)(16-2x)}{2}= \)
\( 16^2-x^2-(8-x)(16-x)= \)
\( -2x^2+24x+128\)
המורה: מצוין.
עידן: אני חישבתי את השטח בדרך אחרת. אפשר לחלק את המחומש הצבוע למשולש ACD ומלבן ABEC, על ידי העברת קו:
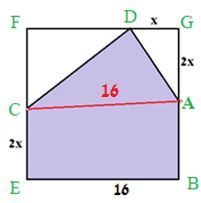
ואז לחשב את שטח המחומש באמצעות סכום של שטח המשולש, כאשר הבסיס שלו הוא 16 כמו צלע הריבוע, ושטח המלבן שנוצר מתחת לקו.
המורה: מדוע בסיס המשולש שנוצר שווה לצלע הריבוע?
האם AB=EC?
דני: ABEC איננו מלבן, מכיוון ש: EC=2x ו- AB=16-2x. לא ידוע לנו שהם שווים!
המורה: האם אפשר לחלק את המחומש אחרת בדומה לדרך של עידן?
רווית: כן, אני מציעה לסרטט קו מקביל לצלע BG דרך נקודה D:
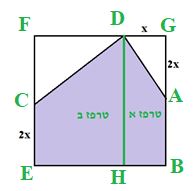
ואז מתקבלים שני טרפזים וניתן לחשב את שטח המחומש כסכום שטחי הטרפזים.
מורה: מה דעתכם, האם זה נכון? בואו נחשב בשתי הדרכים שהוצעו ונשווה את הביטויים.
\( S_{ECDAB}=S_{EHDC}+_{ABHD}= \)
\( =\frac{(16+2x)(16-x)}{2}+\frac{x(16-2x+16)}{2} \)
\(=-2x^2+24x+128\)
- ויזואליזציה מטעה: עידן מסיק מהתבוננות בסרטוט שהקטע AC מקביל לצלע הריבוע EB, כך שנוצר מלבן ABEC.
- הנחה מוטעית: באופן כללי התלמידים לומדים שתי דרכים לחשב שטח של צורות מורכבות. דרך אחת היא לחסר שטחים של “צורות מוכרות” כדי למצוא את השטח שאותו מחפשים (כמו בפתרון של חגית), והדרך השנייה היא לחלק את השטח לצורה פשוטה יותר כמו מלבן ומשולש – כמו שעידן רוצה לעשות. כדי לעשות זאת, עידן מניח פה הנחה שאינה חלק מנתוני השאלה, כי הקטע CA מקביל לצלע BE. אפילו אם עידן היה טוען כי המרובע ABEC הוא טרפז (אותו ניתן לחשב) הוא עדיין היה מתקשה בחישוב ישיר של שטח המשולש ADC.
- המורה שואל את עידן “מדוע בסיס המשולש שנוצר שווה לצלע הריבוע?” כדי לעמת אותו עם הטעות שלו. הוא רוצה לעורר את תשומת הלב של עידן בטעות שלו להניח הנחה לא מבוססת.
- המורה מתייחס אל הדרך של עידן כדרך שמייצגת שיטה נוספת בפתרון בעיות מסוג זה – חישוב שטחים של צורות מוכרות – ומבקש מהתלמידים להציע חלוקה אחרת של השטח.
המורה נותן לגיטימציה לשתי הדרכים: חיסור שטחים, וחיבור שטחים של צורות מוכרות. אפשר לראות בבחירה של המורה להמשיך ולדון בדרכים שונות לפתרון של הבעיה הנתונה כבחירה שנובעת מהרצון לעודד את התלמידים לחשוב על דרכי פתרון רבות, ולא להתייאש כאשר הפתרון לא נכון, אלא לנסות את אותו קו מחשבה (חיבור שטחים) באופנים שונים (לחלק לטרפזים ולא ומשולש ומלבן).
- אפשר לתת לעידן להמשיך לפתור על הלוח בדרך שהציע (מבלי להתערב בדרך):
לחלק את המחומש הסגול למחומש ומלבן, על ידי העברת קו כך: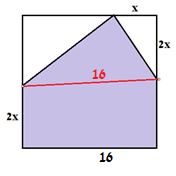
ואז לחשב את שטח המחומש באמצעות סכום של שטח המשולש, כאשר הבסיס שלו הוא 16 כמו צלע הריבוע, ושטח המלבן שנוצר מתחת לקו.
נביע את שטח המלבן באמצעות x: \( S = 16\cdot{2x} = 32x \).
נביע את שטח המשולש שנוצר באמצעות x: \( S=\frac{16⋅2x}{2}=16x \)
שטח המחומש שווה לסכום השטחים של המלבן והמחומש, ולכן שטח המחומש הוא: \( S=32x + 16x=48x \). אם כן, פונקציית המטרה היא: \( y = 48x \).
נגזור את הפונקציה ונשווה את הנגזרת ל-0 על מנת למצוא את ערכו של x, כך ששטח המחומש יהיה מקסימלי \( y’ = 48 \).
בשלב זה, עידן (או חבריו) היו מבחינים בכך, שכאשר משווים את הנגזרת לאפס לא מתקבל פתרון. ואז מתפנים לחקור היכן הייתה השגיאה. דרך אסטרטגיה צריך להגיע למבוי סתום, כדי להיווכח שיש שגיאה -לא מתאים עבור כל משימה. למשל, זה לא היה עובד במקרה שמעלת הפונקציה המתקבלת גבוהה ממעלה ראשונה.
יתרונות באסטרטגיה:
– לא פוסלים מיד את תשובתו של התלמיד, אלא נותנים לו להמשיך עם הרעיון שלו, וניתנת לו הזדמנות להציג את הפתרון שלו (גם אם הוא שגוי). התלמיד יחוש שמכבדים את הרעיונות שלו ונותנים לו במה, ויהיה לו (ולחבריו) אומץ להציג פתרונות שונים גם בהזדמנויות הבאות.
– בדרך זו הבעייתיות בפתרון מתגלה באופן ברור ומידי.
חסרונות באסטרטגיה:
– יש להקדיש לכך זמן מיוחד בשיעור.
– בדרך זו התלמידים רואים רק איך הפתרון לא “עובד”, אבל הם לא מקבלים הסבר מדוע. לא רואים את החובה בהוכחה מסודרת עבור כל הנחה. - אפשר לשלול את הטענה של עידן בעזרת דוגמה נגדית: לסרטט על הלוח

ולשאול:
– האם הסרטוט מתאים לנתונים בשאלה?
– האם בסיס המשולש שנוצר שווה לצלע הריבוע?
– מה המסקנות מכך?
ניתן גם לבקש מתלמידי הכיתה לחפש דוגמה נגדית לטענה שבסיס המשולש שנוצר שווה לצלע הריבוע.
היתרון בדרך זו, שרואים דרכה כיצד מספיקה דוגמה נגדית אחת כדי להפריך טענה.(דוגמה שבה, על אף שהנתונים מתקיימים בסיס המשולש שנוצר לא שווה לצלע הריבוע.) החיסרון בדרך זו הוא שבשימוש בה ללא אסטרטגיית הוראה נוספת, תלמידים לא מבינים מה קורה; מבחינתם, אפשר להביא דוגמה אחרת שבה הטענה כן מתקיימת. התלמידים לא מבחינים בין טענה מתמטית מסוג של “לכל” לבין טענה של “קיים”. כשתלמיד טוען שבסיס המשולש שנוצר שווה לצלע הריבוע לצורך הבעת שטח כללי של המחומש באמצעות \(x\), הטענה שלו בעצם היא מסוג של “לכל”. במילים אחרות, הוא טוען שעבור כל ריבוע שצלעו 16 ס”מ, כאשר מקצים קטע שאורכו \(x\) על הצלע העליונה ושני קטעים שאורכם \(2x\) על הצלעות הצדדיות, הצלע AC שווה 16 ס”מ (ראו סרטוט בסעיף הבא).
דוגמה נגדית אכן מפריכה טענה זו, שכן קיימת דוגמה אחת (לפחות) בה הטענה לא מתקיימת. טענה כזו שונה מטענה מסוג “קיים ריבוע שצלעו 16 ס”מ…”
בסעיף הבא מובאת דוגמה להוספת נתון, שבמקרה שלה קיום דוגמה נגדית לא משליך על אי נכונות של הטענה. מכאן, כדי לשלול את טענת התלמיד באמצעות דוגמה נגדית, לצרכי ההוראה, רצוי לשלב בה אסטרטגיות הוראה נוספות. כמו כן, במקרה זה כדאי גם להדגיש בפני התלמידים את ההבדל בין הטענות משני הסוגים (“קיים” ו-“לכל”). *על שני סוגי הטענות אפשר לקרוא בהרחבה במאמר של צמיר וברקאי, עמודים 40-41.- הוספת נתון: כאסטרטגיה נוספת, ניתן לבקש מן התלמידים להוסיף נתון לשאלה, כך שטענתו של התלמיד תהיה נכונה, ולבקש להוכיח איך הוספת הנתון מצדיקה את הטענה. (הוסיפו אותיות לסרטוט לשם ניסוח קל של הנתונים). דוגמאות לתשובות מתאימות (ללא ההוכחות) שיכולות להתקבל כאן על ידי תלמידים:
- הנקודה A היא אמצע הקטע BG.
- המשולש ACD הוא שווה שוקיים.
- AGD~DFC
- הנקודה D היא אמצע הקטע FG.
- EB || AC
- חלקו את הלומדים לקבוצות. כל קבוצה תקבל אסטרטגיה אחת מבין 3 אסטרטגיות ההוראה המוצעות למעלה. (ללא היתרונות והחסרונות הכתובים כאן). בקשו מכל קבוצה לכתוב יתרונות וחסרונות לאסטרטגיה, ולאחר מכן להציג במליאה את אסטרטגית ההוראה, יתרונותיה וחסרונותיה.
- חלקו את הלומדים לקבוצות. כל קבוצה תקרא אחד המאמרים המצורפים מטה ותדון ביתרונות ובחסרונות של כל אחת מאסטרטגיות ההוראה המוצעות לעיל לאור הרעיונות המוצגים במאמר (צמיר וברקאי 2005) הוא קובץ ארוך ולכן אפשר לבקש שיתייחסו רק לחלקים מהקובץ). במליאה יציגו הקבוצות את תוצרי הקבוצה: יתרונות וחסרונות אסטרטגיות ההוראה לאור הרעיונות המופיעים במאמר.
לסיכום העבודה במליאה נשאל (בשתי ההצעות, א’ ו- ב’):
- במקרה בו הייתה לכם כמורים אפשרות להשתמש רק באסטרטגיה אחת, באיזו מהן הייתם בוחרים ומדוע?
- הציעו אסטרטגית הוראה נוספת.
המשימה המתמטית
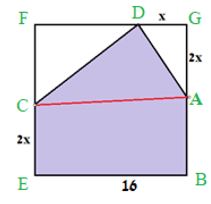
נתון ריבוע BEFG בעל אורך צלע של 16 ס”מ.
מקצים קטע DG שאורכו \(x\) ושני קטעים CE ו- AG שאורכם \(2x\) על הצלעות הצדדיות כמתואר בסרטוט, כך שנוצר המחומש הצבוע.
א. הביעו באמצעות \(x\) את שטחו של המחומש ECDAB
ב. מה צריך להיות ערכו של \(x\) שעבורו שטח המחומש יהיה
מקסימלי?



