ממלבן לריבוע- מציאת שטח מקסימלי

מדוע ינון חושב שהשטח המקסימלי יתקבל כאשר האורך והרוחב שווים?

1. ניסוי וטעיה על סמך אינטואיציה: ינון מנסה לקבל שטח מקסימלי של החלקה על ידי בדיקת זוגות מספרים ומוצא שכאשר האורך והרוחב שווים (כשהמלבן הוא ריבוע), אז השטח הוא מקסימלי.
2. שימוש בחישוב לא מתאים:
   לשם ההוכחה, ינון משתמש בדוגמה לזוג מספרים שבאמצעותם הטענה מתקיימת: \({25}\cdot27<{26}\cdot26 \)
   תוצאה כזו מתקבלת ע”י אחד משני חישובים אפשריים:
   חישוב אפשרי אחד:
   \(        25\cdot27=25\cdot(26+1)=25\cdot26+25\cdot1 \)
   \(        26\cdot26=26\cdot(25+1)=25\cdot26+26\cdot1 \)
   המכפלה בשורה הראשונה קטנה מהמכפלה בשורה השנייה, ולכן אגף שמאל קטן מאגף ימין.

   חישוב אפשרי שני – באמצעות הנוסחה להפרש ריבועים:
   \(        25\cdot27=(26-1)(26+1)=26^2-1^2<26\cdot26 \)
   הפתרון של ינון מבטא גם את הניסיון שלו (מכיתה ט’) בקביעת סימן אי השוויון בין ביטויים אלגבריים עם פרמטרים.
   עבור \(       (a-b)(a+b)<a\cdot a \) כאשר \(       a,b\neq 0 \)
   כיוון ש \(       (a-b)(a+b)=a^2-b^2 \) ו- \(      a^2-b^2<a^2 \).
   כלומר, המכפלה המקסימלית מתקבלת כאשר גורמי המכפלה הם שווים במקרה כזה.

3. הסתמכות על מקרה פרטי: לניסוח הטענה, ינון משתמש בדוגמה ספציפית במקום הוכחה. הוא סבור שאם טענה נכונה עבור דוגמה אחת של זוג מספרים (או יותר), אז היא חייבת להיות נכונה עבור כל המקרים.
4. התבססות על ניסיון קודם: ינון זוכר מפעילויות קודמות שלמד בכיתה ט’ או י’ ששטחים מקסימליים מתקבלים בצורות משוכללות. בפעילויות אלה דנים על צורות שוות היקף שהשטח שלהן שונה, או צורות שוות שטח שההיקף שלהן שונה, ומסיקים מסקנות לגבי ההיקף או השטח.

1. ינון מציע פתרון שמתאים למקרה מסוים של ריבוע (או מצולעים משוכללים), בו השטח מקסימלי. במקרה זה, המורה בוחר להתייחס להצעה של ינון רק לאחר שפתר את השאלה בדרך הנהוגה על ידי בניית פונקציית מטרה, שהיא שלב מוקדם בתהליך פתרון בעיות קיצון (לפני גזירה ומציאת נקודת הקיצון). אם נושא זה, של בעיות קיצון, עוד לא נלמד בכיתה, הבחירה של המורה בפתרון על דרך זו נועדה למנוע בלבול בהמשך, בייחוד בפתרון שאלות אחרות באותו נושא (בהמשך ילמדו את שאר הפרוצדורה ויכירו את שאר המקרים הרבים של בעיות קיצון).
2. המורה כן מתייחס לפתרון של ינון, כי הוא מזהה בו מחשבה מקורית ומעוניין לעודד אותה. הוא עושה זאת ע”י חקירה משותפת את הדרך בה הגיע ינון לפתרון, כדי להדגיש בפני הכיתה את החשיבות במחשבה עצמאית ויצירתית בפתרון משימות. בכך, הוא מסמן לשאר התלמידים שיש מקום לשתף מחשבות שכאלה בכיתה ושהן זוכות להכרה חיובית.
3. המורה מבקש מינון להוכיח את הטענה שלו עבור מקרים נוספים, מעבר לדוגמה שנתן. הוא עושה זאת כדי לעמוד על העיקרון שדוגמה ספציפית לא מספיקה ורק הוכחה פורמלית מתקבלת.

מאירוע זה עולה החשיבות בדיון על חובת הוכחה פורמלית, ושדוגמה אחת, ואפילו דוגמאות רבות, לא מספיקות כדי להוכיח נכונות של טענה. אפשר לעשות זאת בכיתה דרך הצגה של טענה אחרת (לא נכונה) שמתקיימת עבור דוגמה מסוימת, ולאחר מכן להביא דוגמה נגדית, או לבקש מן התלמידים למצוא כזו.
למשל, טענה שמתקיימת עבור דוגמה ספציפית יכולה להיות: אם אלכסוני מרובע שווים זה לזה, אז המרובע הוא מלבן. ניתן גם לצייר דוגמה:

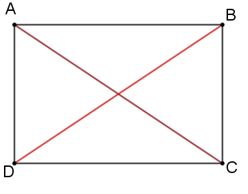
הטענה מתקיימת לגבי המרובע שבסרטוט, שכן האלכסונים בו שווים והמרובע הוא מלבן. דוגמה זו, אין בכוחה להשליך על הכלל ולהוכיח פורמלית את הטענה כי כל מרובע בעל אלכסונים שווים הוא מלבן. נביא דוגמה נגדית לכך בסרטוט של טרפז שווה שוקיים, בו האלכסונים אמנם שווים, אך הוא איננו מלבן. (דוגמה שממחישה אי נכונות הטענה). מכאן שלא כל מרובע שאלכסוניו שווים זה לזה הוא מלבן.

1. חלקו את הלומדים לקבוצות, בהן ינסו להוכיח את הטענה של התלמיד דרך בדיקת המספרים השונים. כל זאת, בלי שקראו קודם את תגובת המורה.
2. בקשו מהלומדים להביא דוגמה לטענה לא נכונה ודוגמה נגדית שהשתמשו בה בכיתה שלהם כשהיו צריכים להמחיש את חשיבות ההוכחה פורמלית.
3. דונו עם הלומדים: באיזה שלב בכיתה לדעתם, כדאי להתייחס לפתרון כזה של תלמיד בהקשר של האירוע הזה? התייחסו ליתרונות ולחסרונות של כל הצעה.
4. דונו ביתרונות ובחסרונות המשימה שבאירוע כמשימה לפתיחת הנושא של בעיות קיצון בכיתה. שימו דגש על השאלה: מה האפשרויות השונות של למידה והרחבת הידע המתמטי של התלמידים, שמשימה זו מזמנת?
   באופן כללי, צורות הצגה של משוואת הפרבולה ומציאת קודקוד הפרבולה בייצוגים השונים.
   במקרה זה, התשובה של ינון למשימה, למשל, פתחה פתח לדיון כולל על הקשר בין צורות משוכללות ושטח מקסימלי (כאשר ההיקף נתון).
   החיסרון בהצגת משימה זו בפתיחת הנושא הוא שהפתרון יכול להיות מהיר (כפי שקרה באירוע), כך שאפשר לאבד בדרך את הצורך בשיטה לפתירת בעיות קיצון. כדי להתגבר על כך, מומלץ לבחור משימה שבה מגיעים למשוואה ממעלה שלישית, שבה קבלת נקודת הקיצון היא כבר פחות אינטואיטיבית.

גילה, ח’ . (1994) .מספר היבטים פדגוגיים של ההוכחה. על”ה, 14. 7-11.