פיצול הפונקציה לשני תחומים כאשר יש ערך מוחלט
תיאור האירוע
מתרגלים בכיתה לקראת מבחן. בתחילת השיעור, שירה מבקשת מהמורה לפתור יחד את סעיף ג (1) במשימה, שלא הצליחה לפתור בבית.
המורה: בואי תציגי על הלוח את הפתרון שלך.
שירה משרטטת סקיצה של הפונקציות הנתונות, וכן קטע \(AB\) כלשהו שנדרשים למצוא את אורכו המקסימלי.
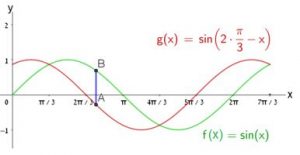
שירה: הקטע \(AB\) מקביל לציר ה- \(y\), לכן לנקודות \(A\) ו \(B\) שיעור ה-\(x\) זהה. משום שלא ידוע איזו נקודה נמצאת מעל השנייה, נצטרך להוסיף סימן של ערך מוחלט להפרש בין שיעורי ה \(x\) של שתי הנקודות.
מכאן, אורך הקטע \(AB\) הוא \(AB=|sin(\frac{2\pi}{3}-x)-sin x|\) ופונקציית המטרה בסעיף זה היא: \(y=|sin(\frac{2\pi}{3}-x)-sin x|\).
המורה: עד כאן הפתרון שלך מצוין. איפה נתקלת בבעיה?
שירה: כאשר גזרתי וחיפשתי נקודת מקסימום, לא מצאתי נקודה כזאת, כי קיבלתי שהנגזרת מקבלת תמיד ערכים חיוביים.
המורה: מה הנגזרת שקיבלת?
שירה: \(y’=|-cos(\frac{2\pi}{3}-x)-cos x|\).
השוויתי את הנגזרת ל- 0 וקבלתי: \(x=\frac{5\pi}{6}\space\space,\space\space x=\frac{11\pi}{6}\).
כשאני מציבה אותם בטבלה, הנגזרת מקבלת רק ערכים חיוביים, בגלל הערך המוחלט.
המורה: בואו נסתכל על פונקציה פשוטה יותר עם ערך מוחלט \(y=|x|\).
נראה את הסרטוט שלה:
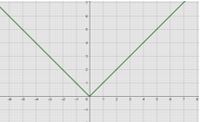
לפי דרך הפתרון שלך, הנגזרת של פונקציה זאת היא 1.
שירה: נכון, אבל בציור רואים שברביע השני השיפוע של הפונקציה הוא 1-, כלומר הנגזרת בחלק זה היא 1-.
המורה: למה זה כך?
שירה: כי צריך לפצל את הפונקציה לשני תחומים שונים:
עבור \(x\ge 0\) הפונקציה היא \(y=x\), ועבור \(x\le 0\) הפונקציה היא \(y=-x\).
בפונקציה זו עבור ערכי x שליליים ערכי ה y הם חיוביים.
המורה: יפה. אז נסכם, פונקציית הערך המוחלט היא בעצם שתי פונקציות ש…
שירה: אה הבנתי! הטעות שלי היא בנגזרת. הייתי צריכה לגזור את הפונקציה לפי שני מקרים:
כאשר הנקודה \(B\) נמצאת מעל הנקודה \(A\) צריך לגזור את הפונקציה \(y=sin(\frac{2\pi}{3}-x)-sin x\).
כאשר הנקודה \(A\) נמצאת מעל הנקודה \(B\) צריך לגזור את הפונקציה \(y=sin x-sin(\frac{2\pi}{3}-x)\).
המורה: נכון.
שירה מבחינה נכון, כבר כשהיא פותרת בבית, שצריך להוסיף לאורך הקטע AB סימן של ערך מוחלט, כיוון שלא ידוע איזו נקודה נמצאת מעל השנייה (כמו ביישומון בו רואים את האפשרויות השונות לאורך הקטע AB).
היא מבינה את המשמעות של סימן הערך המוחלט במובן של אורך קטע, אבל היא לא מבינה את משמעות הסימן כאשר הוא נמצא בתוך פונקציה שצריך לפצל לשתיים.
שירה גוזרת את פונקציית המטרה שהתקבלה מבלי לפצל אותה לשני תחומים נפרדים. היא גוזרת את הפונקציה שבתוך הערך המוחלט ומוסיפה לנגזרת את סימן הערך המוחלט, כך שהוא הופך את ערכי הנגזרת לחיוביים, למרות שלא כך המצב.
דוגמה פשוטה שמביאה המורה עוזרת לה להבין את מקור הטעות שלה ואיך לפתור אותה.
- המורה, בשיתוף עם שירה, עוברת איתה על דרך הפתרון שלה שלב אחר שלב, עד שיגלו באיזה שלב טעתה. המורה לא נותנת את הפתרון במליאה, וגם לא מצביעה על הטעות של שירה בפיצול הפונקציות. היא משקפת לה את דרך הפתרון שלה דרך בחירה בפתרון של בעיה פשוטה יותר מסוג דומה, וכך מתבהר לשירה מדוע בפונקציה \(y=|x|\) הנגזרת אינה 1 בלבד, אלא צריך לפצל את הפונקציה לשתי פונקציות שונות, והנגזרת משתנה בהתאם לכך.
2. ככל שהמורה מובילה את שירה בשאלות מכוונות, היא תורמת להעמקת ההבנה שלה ושל שאר התלמידים בכיתה על הצורך לפצל פונקציות כאשר נתונה פונקציה עם ערך מוחלט.
דרך נוספת לפתור את המשימה היא לבנות את פונקציית המטרה ללא ערך מוחלט: \(y=g(x)-f(x)=sin(\frac{2\pi}{3}-x)-sin x\).
נגזור את הפונקציה ונקבל \(y’=-cos(\frac{2\pi}{3}-x)-cos x\).
נשווה לאפס ונמצא את שיעור האיקס של נקודות הקיצון וסוגן. נקבל \(x=\frac{11\pi}{6}\) מקסימום, ו- \(x=\frac{5\pi}{6}\). במליאה נשאל את התלמידים שאלות מנחות שמטרתן להגיע למסקנה, שגם בנקודת המינימום של פונקציית המטרה מתקבל מרחק מקסימלי.
פונקציה המטרה מנוסחת לפי \(y=g(x)-f(x)\) (בחירת סדר הפונקציות בפעולת החיסור היא שרירותית), ולכן כאשר \(f(x)\) נמצאת מעל \(g(x)\), נקבל ערך שלילי, שהוא הקטן ביותר עבור הפונקציה (נובע מהבחירה השרירותית בסדר הפונקציות). אפשר לשאול את התלמידים:
א. עבור איזו נקודה נקבל מרחק מינימלי, הקצר ביותר? (נדגיש שמרחק לא יכול להיות שלילי).
ב. עבור איזו נקודה נקבל מרחק מקסימלי?
ג. מה הייתה פונקציית המטרה עבור \(y_{A}>y_{B}\)? מצאו את נקודות הקיצון עבור פונקציה זו.
ד. מה הייתה פונקציית המטרה עבור \(y_{A}<y_{B}\)? מצאו את נקודות הקיצון עבור פונקציה זו.
ה. השוו בין התשובות שקיבלתם בשני הסעיפים, ג’ ו- ד’ והסבירו את ממצאיכם.
אפשר להשתמש בדרך הפעולה האלטרנטיבית עם הלומדים, ולתת להם להסביר כיצד המינימום של פונקציית המטרה מוביל למרחק מקסימלי בעצמם.
המשימה המתמטית
מתוך בחינת הבגרות קיץ 2013, מועד א’ שאלון 581:
נתונה הפונקציה \(g(x)=sin(\frac{2\pi}{3}-x)\) בתחום \(0≤x≤\frac{7}{3} \pi\).
א. מצא את נקודות החיתוך של גרף הפונקציה \(g(x)\) עם הצירים.
ב. מצא את השיעורים של נקודות החיתוך של גרף הפונקציה \(g(x)\) עם גרף הפונקציה \(f(x)=sinx\).
ג. הנקודה \(A\) נמצאת על גרף הפונקציה \(g(x)\) והנקודה \(B\) נמצאת על גרף הפונקציה \(f(x)\), כך שהקטע \(AB\) מקביל לציר ה- \(y\).
(1) מצא את האורך המקסימלי של הקטע \(AB\).
(2) כמה קטעים כמו \(AB\) שאורכם מקסימלי מתקבלים בתחום הנתון? נמק.


