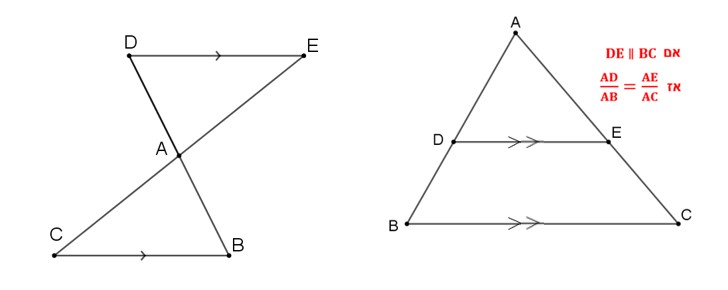
הרחבות למשפט תאלס
תיאור האירוע
בתחילת השיעור המורה כותבת את המשפט על הלוח לתזכורת לשיעור הקודם. (התלמידים מתבקשים לנסח את המשפט ההפוך).
מעיין: אוקיי, אפשר אולי להגיד שאם מתקיים היחס \( \frac{AD}{AB}=\frac{DE}{BC} \) אז הישרים מקבילים?
המורה: מעניין, אפשר לנסח את השאלה של מעיין כטענה מתמטית: אם \( \frac{AD}{AB}=\frac{DE}{BC} \) אז DE || BC. איך נבדוק אם הטענה נכונה? מה הכלי המתמטי שיש לנו?
[ מחכה כמה שניות].
אנחנו צריכים להוכיח אותה. בעצם נתייחס לטענה שלנו כאל “הנתון” בשאלה ונראה אם אנחנו מצליחים להגיע למסקנה ש- DE || BC. יש לכם רעיון איך לעשות את זה?
אני מציעה שתתחילו לעבוד על זה בזוגות. אני רק מזכירה לכם שכדי להוכיח טענה יש להראות את הנכונות שלה באופן כללי, להפרכה של טענה מספיקה דוגמה נגדית.
התלמידים עובדים בזוגות. כעשר דקות לפני סוף השיעור חוזרים למליאה להצגה.
נויה: [ניגשת ללוח, משרטטת ומסבירה] לדעתי אפשר להפריך את הטענה ככה:
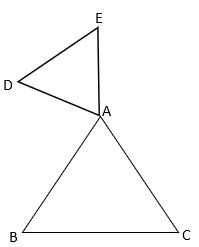
במקרה הזה, אם למשל המשולשים דומים, אז היחס מתקיים, אבל הישרים DE ו- BC לא מקבילים!
המורה: יפה מאוד! רעיון מאוד יפה! [לכיתה], מה אתם חושבים על ההסבר של נויה?
תלמידים: יפה מאוד!
המורה: אני גם חושבת שזה רעיון יפה, יש פה רק בעיה קטנה. מי יודע להגיד מה הבעיה?
ירדן: אולי זה לא קשור למשפט ההפוך למשפט תאלס? אין לי ממש מושג, פשוט זה נושא השיעור…
המורה: הכיוון שלך נכון, ירדן. הטענה של מעיין היא ווריאציה למשפט ההפוך למשפט תאלס. המשפט ההפוך למשפט תאלס מדבר על שני ישרים החותכים שוקי זווית או את ההמשך של שוקיי הזווית. כלומר, על אחד משני המצבים הבאים:
המורה: עוד רעיונות?
לוטן: אני חשבתי ככה. אני יכולה לבוא להסביר?
המורה: בטח, בואי.
לוטן נגשת ללוח ומסרטטת:
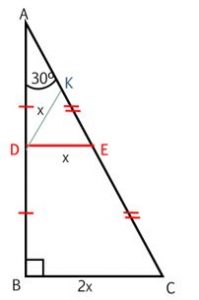
לוטן: משולש ABC הוא משולש 90° ,60° ,30°. נעביר את DE קטע אמצעים במשולש ונסמן אותו ב- \(x\).
אם DE שווה ל– \(x\) אז BC שווה ל- \(2x\) BC. היא הצלע מול ה- 30 מעלות במשולש ישר זווית, ולכן היא שווה למחצית היתר. היתר כולו הוא \(4x\) ו- AE ו- CE שווים ל- \(2x\) כל אחד.
לפי הבניה, משולש ADE דומה למשולש ABC. נעביר מקודקוד D תיכון ליתר AE ונסמן אותו ב-DK. במשולש ישר זווית התיכון ליתר שווה למחצית היתר ולכן DK גם שווה ל- \(x\). אז עכשיו קיבלנו ש:
\( \frac{AD}{AB}=\frac{DK}{BC}=\frac{1}{2} \)
אבל DK ו- BC אינם ישרים מקבילים!
- מעין לא מציעה את המשפט ההפוך, אלא מנסה להציע וריאציה שלו. היא מנסה להרחיב את המשפט ההפוך מעבר לניסוח שהופך בין “אם” ל-“אז”, שנראה לה טריוויאלי. היא מנסחת אותו כאילו היה מדובר בשלשה פרופורציונית, בגלל הידע הקודם שיש לה בדמיון ובפרופורציה של משולשים.
היא נוטה לחשוב, שכאשר יש שוויון יחסים בין שני זוגות של צלעות, אז גם הזוג השלישי מתייחס אחד לשני באותה פרופורציה. לכן, מבחינתה, שוויון יחסים של שני זוגות מספיק כדי לקבוע שצלעות מקבילות.
הטעות של מעיין נובעת מכך שהיא לא מתייחסת לכך שהקטעים נמצאים על שוקי הזווית. - נויה רואה את ההבדל בין ההרחבה למשפט תאלס ההפוך ובין שלשה פרופורציונית. היא משתמשת בידע שלה מדמיון משולשים כדי להפריך את הטענה של מעין: היא מניחה ששני המשולשים דומים, כדי להראות שיחס פרופורציוני בין שני זוגות של צלעות לא גורר הקבלה של הזוג השלישי. עם זאת, היא מתעלמת מנתון “סמוי” העומד בבסיס משפט תאלס, שהוא המצב שבו שני ישרים חותכים שוקי זווית אן את ההמשך של שוקי הזווית.
- לוטן מבססת את הפתרון שלה על משולש מיוחד – משולש ישר זווית עם זווית חדה של 30 מעלות – שמקיים סט רחב של תכונות. בנוסף, הרעיון שלה מאמץ רעיון שעלה בדרך של נויה – הסטה. לוטן מסיטה את צלע המשולש הפנימי בזווית וכך מספיקה לה דוגמה אחת כדי להפריך את הטענה.
- המורה מזהה באירוע הזדמנות לחקירה של טענה שנראית הגיונית אבל לא בהכרח נכונה. וכך היא מחליטה לסטות מהמהלך המתוכנן של השיעור ולאפשר לתלמידים להתמודד עם הוכחת הטענה.
- המורה רוצה להמחיש לתלמידים את כוחה של הוכחה ככלי לבדיקת נכונות טענות. כל “משפט” שהתלמידים מוכיחים הוא טענה הניתנת לבדיקה. בדרך כלל, התלמידים בודקים נכונות טענות שכתובות להם בספרים, והן בדרך כלל נכונות. כאן יש להם ההזדמנות לבחון נכונות של טענה שלא ידוע מראש אם היא נכונה או לא – טענה שעלתה מתוך סקרנותם הטבעית של התלמידים. היציאה לחקירה של טענה לא מוכרת מעוררת את הכיתה לעשייה ומעודדת אותם להפעיל את כל הכלים הגיאומטריים שלהם.
- הרעיון העומד בבסיס הפרכת הטענה הוא שישנו מצב שנשמר – שני ישרים שמקצים קטעים פרופורציוניים על שוקי זווית. ניתן לבקש מהתלמידים לחשוב על משפטים הפוכים נוספים, שכדי לנסח אותם נכון צריך לכלול בניסוח מצב מסוים חייב להישמר בשני הכיוונים.
למשל, משפט חוצה זווית ההפוך: על מנת שהמשפט “אם \( \frac{CD}{BD}=\frac{AC}{AB} \) אז \( \measuredangle CAD=\measuredangle BAD \)” יהיה נכון, יש לציין שעוסקים בקטע המחבר קודקוד במשולש עם הצלע שמולו, כמו בסרטוט הבא: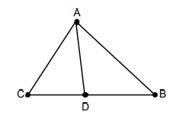
פעילות מהסוג הזה מאמנת את התלמידים לזהות מהו הנתון המהווה “מצב שנשמר” (משולש שבו קטע מחבר בין הקודקוד לצלע מולו), גם אם אינו כתוב באופן מפורש. באופן זה, המעבר למשפט הפוך יעשה בצורה הנכונה, ולא יצוצו הנחות שגויות בדרך.
הצעה לדרך עבודה על משימה בגיאומטריה: לבקש מהתלמידים לשרטט סרטוט מתאים לטענה של מעיין, ועל בסיסו לפתח את ניסיונות ההוכחה לפי “חוקי המשחק” של אותו מצב. דיון כזה ביכולתו לעורר יותר תלמידים לעשייה, גם כאלו שמרגישים שאין בכוחם להתמודד עם טענה ללא סרטוט. לאחר שמסכימים על הסרטוט שרלוונטי לנתוני הבעיה, אפשר לבקש מהתלמידים להעלות את כל המידע שנראה להם רלוונטי ונובע מהמשימה, ולבסוף לאפשר להם להוכיח את הטענה המופיעה במשימה באופן עצמאי. בפעילות מהסוג הזה מרוויחים מצד אחד סקירה של תכונות גיאומטריות רבות וגם מתקיים דיון על הרלוונטיות של כל תכונה לפתרון המשימה.
- הציגו את הטענה של מעיין ללומדים. בקשו מהם לחוות דעתם – האם הטענה של מעיין נכונה. בקשו מהם להוכיח או להפריך אותה. הציגו את ההוכחות במליאה, בדיוק כמו שהתרחש בכיתה. במידה והם לא מגיעים למסקנה נכונה ניתן להציג את שתי הדוגמאות הנגדיות – של נויה ושל לוטן – ולשאול אותם מה דעתם על כל אחת מהדוגמאות, ואיזו דוגמה מתאימה להפרכת הטענה.
- הרעיון שעומד בבסיס הדוגמה להפרכת הטענה הוא שישנו מצב שנשמר – שני ישרים שמקצים קטעים פרופורציוניים על שוקי זווית או על ההמשך שלהם. אפשר לבקש מן הלומדים לקרוא את המאמר בחלק הבא, ולדון במצבים הנוספים בהם הסתכלות על מה נשמר ומה משתנה בין המצבים השונים במשימה משפיעה על איך התלמידים מבינים ומתמודדים עם משימה.
המשימה המתמטית
נסחו את המשפט ההפוך למשפט תאלס המורחב:
ישר המקביל לאחת מצלעות המשולש חותך את שתי הצלעות האחרות או את המשכיהן בקטעים פרופורציוניים