חישוב שטח משולש או חישוב אינטגרל?
תיאור האירוע
שיעור חזרה לקראת בחינת הבגרות (פתרון סעיף ג’ במשימה).
התלמידים מתבקשים לפתור באופן עצמאי את המשימה.
דני: מצאתי ששיעורי נקודה A הם \( (4,0)\) ושיעורי נקודה B הם \((3,5) \). חישבתי את השטח המבוקש לפי גובה המשולש (שיעור \(y \) של הנקודה B) כפול אורך הצלע שלו \( (4=AO)\) חלקי שתיים. לכן, שטח המשולש הוא \( \frac{4\cdot5}{2} \), כלומר 10 סמ”ר.
המורה מציג את הפתרון של דני במליאת הכיתה ושואל: מה דעתכם על הפתרון? מה אתם חושבים? הסבירו את התשובה שלכם.
בכיתה מתפתח דיון על נכונות הפתרון, במהלכו המורה מסביר שחישוב זה אינו מדויק, כיוון שצורת הפרבולה היא קו עקום, וצלע של משולש היא קטע שהוא חלק מהישר.
דני מחשב את שטח המשולש OBA כאילו היה השטח המבוקש.
1. ויזואליזציה שמטעה: הסרטוט מטעה – חלק הפרבולה הנדון נראה כמו קטע ולא כמו עקום שהוא חלק מפרבולה. דני, שמסתמך על הסרטוט מסיק בטעות שהשטח שיש לחשב הוא, למעשה, משולש.
2. חוסר תשומת לב והיעדר בקרה: דני לא מתייחס לנתוני השאלה. הוא מתעלם מכך שהגרף הנתון הוא גרף של פונקציה ריבועית והקטע AB הוא קטע על פרבולה. לו היה מיישם את נתוני השאלה, היה מחשב את השטח בעזרת אינטגרל.
- המורה בוחר להדגיש את השגיאה של דני במליאה. חשוב לו להסב את תשומת לב כולם לשגיאה, כדי למנוע הישנותה בבחינה המתקרבת.
- המורה מבקש השתתפות התלמידים בהסבר מקור השגיאה. חשוב לו לחזור עם התלמידים על אינטגרל מסוים כדרך לחישוב שטחים. הוא רוצה שהתלמידים יבחינו בעצמם כי העקום בין הנקודות A ו- B הוא קטע על הפרבולה, ושאין לחשב שטח מתחת לעקומה כאילו היה שטח משולש.
- המורה רוצה להעלות את מודעות התלמידים לחשיבות של ביצוע ביקורת על הפתרון. להזכיר לתלמידים כי במהלך פתרון תרגיל יש לקרוא את הנתונים היטב, ובסיומו יש לחזור לנתונים ולראות שאכן התייחסו אליהם נכון וכן שפתרו את הבעיה שהתבקשו לפתור.
שימוש בתוכנת GeoGebra
בהמשך לפעולות המורה, ניתן היה לדון במשמעות של חישוב אינטגרל מסוים בדרכים הבאות:
- לחזור על הסבר העוסק במהות החישוב של אינטגרל מסוים בעזרת אינטגרל (קישור לישומון).
- לדון בהפרש בתוצאות שבין שני החישובים – חישוב שנעשה בעזרת הנוסחה למציאת שטח משולש מול החישוב שנעשה בעזרת אינטגרל מסוים – ולהמחיש את ההפרש ביישומון.
בעזרת היישומון אפשר להזיז את נקודה B ולבחון יחד כיצד הטעות בקירוב בין נוסחת שטח המשולש לבין חישוב השטח בעזרת אינטגרל גדלה או מתי קטנה בהתאמה, כתלות בנקודה B (אפשר לתת לתלמידים להתנסות ולהסביר את תוצאות החקר).
המחשת הממצאים מהשימוש ביישומון בסרטוטים מטה: הנקודה מוזזת והשטח משתנה בהתאמה – ההפרש בין השטח המבוקש לשטח המשולש משתנה עם כל הזזה של הנקודה על הגרף. (ההפרש הקטן ביותר מתקבל כאשר שיעור האיקס של נקודה B הוא 3, כפי שנתון בשאלה).
בסגול – השטח שחושב בעזרת נוסחה לשטח משולש.
בורוד – השטח המבוקש שחושב בעזרת אינטגרל מסוים.



להרחבה: ניתן לחקור יחד עם התלמידים את שגיאת החישוב של אינטגרל רימן הנעשה באמצעות מלבנים אל מול שגיאת החישוב המשתמשת בקירובים של צורות אחרות, למשל טרפזים (שיטת הטרפזים).
מה יכולים להיות היתרונות ו/או החסרונות של שיטות קירוב שונות? דיון כזה יתחיל מתוך הבעיה הנתונה, תוך ניסיון של שימוש בשיטת המלבנים או הטרפזים באופן אינדוקטיבי ומשם ניסיון להכליל לגבי התובנות המתמטיות.
מטרת הפעילות: העמקה בתפיסה מוטעה של תלמידים וניסוח דרכי תגובה אפשריות של המורה
ערכו דיון עם הסטודנטים על האירוע. השתמשו בשאלות:
א. מה היה באירוע? מדוע אירוע זה הוא אירוע קריטי, לדעתכם?
ב. מה התלמיד אמר/עשה?
ג. מה הסיבה לדעתכם לשגיאה של התלמיד?
ד. מה מורה יכול לעשות במצב כזה?
ה. האם כדאי למורה לחזור למשמעות של האובייקטים המתמטיים, או שעליו להסתפק בתיקון השגיאה? מה היתרונות ומה החסרונות של חזרה על משמעות האינטגרל ומה היתרונות והחסרונות בתיקון השגיאה בלבד?
מערכי שיעור להוראת נושא חישובי שטחים (מתוך אתר רמזור)
המשימה המתמטית
(שאלון 841, חורף 2011, מועד מיוחד ללוחמים)
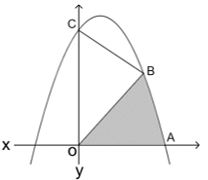
בסרטוט שלפניך נתונה הפרבולה \(y=-x^2+2x+8\).
A ו- C הן נקודות החיתוך של גרף הפונקציה עם הצירים.
א. מצא את שיעורי נקודות A ו- C.
ב. נתון כי B היא נקודה על גרף הפונקציה ברביע הראשון
כך ששטח המשולש OBC הוא 12 סמ”ר (O- ראשית הצירים).
מצא את שיעורי הנקודה B.
ג. מצא את השטח המוגבל על ידי גרף הפונקציה,
על ידי הישר BO ועל ידי ציר \(x\).