ההבדל בין אינטגרל מסוים לבין שטח
תיאור האירוע
תרגול שאלת בגרות משאלון 581 מועד חורף 2019 בנושא חקירה ואינטגרל של פונקציית מנה.
המורה מבקשת מהתלמידים לפתור בעצמם את השאלה לפני שיפתרו אותה יחד על הלוח. היא מסתובבת בין התלמידים בעת התרגול ורואה שמצאו נכון את הביטוי של הפונקציה \(g(x)=-\frac{3}{x^2} +\frac{3}{(x-4)^2}\) וסרטטו את הסקיצות הבאות:
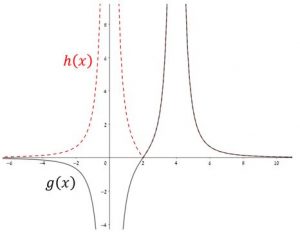
בפתרון בסעיף ג אצל מספר תלמידים המורה מבחינה בשגיאה. היא מבקשת מאחת התלמידות ששגו לגשת ללוח ולהציג את הפתרון שלה.
יעל: נתון ש- \(h(x)=|g(x)|\) ונתון ש- \(\int_{a}^{2}g(x)dx=t\)
(מציגה את הסרטוט של הפונקציות מסעיף ב’ על הלוח).
זו הסקיצה של \(h(x)\) ו- \(g(x)\) באותה מערכת צירים.
התבקשנו לחשב את האינטגרל \(\int_{a}^{2}(h(x)-g(x))dx\), אז נוסיף לסקיצה את הישר \(x=a\) כדי לראות את השטח המבוקש:
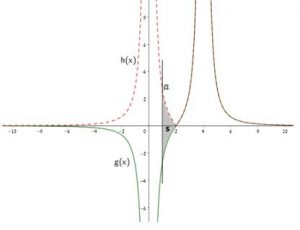
\(\int_{a}^{2}h(x)dx=\int_{a}^{2}g(x)dx\)
כיוון שהשטח בין גרף הפונקציה \(h(x)\) לבין ציר ה- \(x\) הוא שיקוף של השטח בין ציר \(x\) לבין גרף הפונקציה \(g(x)\) בגבולות אלה, אז השטחים שווים, ולכן \(\int_{a}^{2}(h(x)-g(x))dx=2\int_{a}^{2}g(x)dx=2t\).
המורה: מה זה \(t\)?
בואו נתבונן שוב באינטגרל הנתון – \(\int_{a}^{2}g(x)dx=t\) בתחום \(0<a<2\). היכן נמצאת הפונקציה \(g(x)\)?
מיכל: בתחום זה גרף הפונקציה \(g(x)\) נמצא מתחת לציר \(x\), ולכן הפונקציה היא שלילית.
המורה: מה זה אומר לגבי הפונקציה \(h(x)\)?
תלמידים: שבתחום זה מתקיים \(h(x)=-g(x)\) כיוון ש- \(h(x)=|g(x)|\).
המורה: כיצד זה משפיע על הפתרון שלנו?
רועי: שאפשר לכתוב את האינטגרל ככה:
\(\int_{a}^{2}(h(x)-g(x))dx=\int_{a}^{2}(-g(x)-g(x))dx= \int_{a}^{2}(-2g(x))dx=-2\int_{a}^{2}g(x)dx\).
ולקבל: \(\int_{a}^{2}(h(x)-g(x))dx=-2t\)
המורה: יפה מאוד!
- בלבול מושגים: יעל מבלבלת בין המושגים “אינטגרל מסוים” ו”שטח”. על פי רוב, תלמידים נדרשים למצוא שטח ולא רק אינטגרל מסוים. במקרה זה, יעל מסיקה שמדובר בשטח, ושהשטח המוגבל בין גרף הפונקציה \(g(x)\) לבין ציר ה-\(x\) בתחום \(0<a<2\) שווה ל \(t\).
כידוע, אינטגרל לא מתייחס לשטח בלבד. לפי משפט ניוטון לייבניץ, הגדרת אינטגרל מסוים כוללת חישוב פונקציה קדומה בתחום מסוים, ולכן לא ניתן לצפות לקבלת תוצאה חיובית בלבד. (האינטגרל המסוים מסמן שטח רק כאשר הוא נעשה על פונקציה בתחום בו היא חיובית). - יעל לא מחשיבה את האפשרות שהפרמטר t יכול לייצג גם מספר שלילי. כיוון שהיא טועה לראות פרמטר זה כמייצג מספר חיובי, היא מסיקה מכך שנדרש ממנה לחשב שטח.
המורה שואלת את יעל והתלמידים שאלות מכוונות: מה זה \(t\)? היכן נמצאת הפונקציה \(g(x)\)? מה זה אומר לגבי הפונקציה \(h(x)\)? וכו’, כדי שיעלו על השגיאה בעצמם.
המורה בוחרת להימנע מלמסור לתלמידים מיד את הפתרון, מתוך אמונה שזו הדרך לקדם את הכיתה לקראת למידה משמעותית והבנה טובה יותר של הנושא.
- אפשר להשתמש במושגים אינטגרל מסוים ושטח ולערוך עם התלמידים הבחנה מפורשת ביניהם, במטרה לחדד את מקור השגיאה. בדומה, אפשר גם לחדד את היתכנות ערך שלילי לפרמטר \(t\).
- אפשר להציג לתלמידים משימות שונות בנושא אינטגרלים, ולבקש מהם למיין את המשימות לפי תתי נושאים: סוג המשימה, לפי מציאת שטח, מציאת אינטגרל מסוים וסוג התשובה המתקבלת, לפי מספר חיובי, מספר ממשי ומציאת אינטגרל לא מסוים ממשפחה של פונקציות (קדומות), אשר משתנה לפי ערך הקבוע c. לאחר שמוינו, אפשר להחליט יחד מה סוג התשובה המתאים לכל קבוצת משימות באמצעות טבלה.
אפשר לבצע את הפעילות בקבוצות, בה התלמידים מקבלים לפתור משימה אחת מכל סוג ובסיום הפעילות מציגים עבודתם במליאה ודנים בהבדלים בין שלושת סוגי המשימות.
אפשר לפני הפעילות לפתוח את השיעור בדיון.
מטרת הפעילות ללמד את התלמידים לזהות בכל משימה בנושא אינטגרלים מהי סוג המשימה, ומה המשמעות של סוג המשימה על דרך הפתרון שלהם ועל התשובה שאמורים לקבל, כדי להתמודד טוב יותר עם פתרון משימות מסוג זה בעתיד.
- הזמינו את הלומדים למשימת חקר, בה יסקרו ספרי לימוד שונים ומקורות אחרים, כדי לראות כיצד מוגדר בהם ההבדל בין אינטגרל מסוים לבין שטח מתחת לעקומה. (כמשימה לבית, או לגשת לספריה בזמן השיעור/פעילות)
דוגמאות מספרי לימוד/מקורות:
– בני גורן מתייחס לכך שאינטגרל מסוים הוא חישוב של פונקציה קדומה בגבולות מסוימים וחישוב שטח הוא שימוש של אינטגרל מסוים.
– בספר “ללמוד וללמד אנליזה” מתחילים את ההסבר מתוך השימוש באינטגרל מסוים לחישוב שטח ומתייחסים לפונקציה אי-שלילית.
– בויקפדיה כתוב “האינטגרל המסוים של פונקציה אי־שלילית המוגדרת על קטע סופי, הוא מספר השווה לשטח הכלוא בין ציר ה-\(x\), לבין גרף הפונקציה, בין קצוות הקטע”. - ערכו דיון על הממצאים שיביאו הלומדים ממחקרם. דונו בחשיבות של חידוד הבדל זה לתלמידים מתוך הממצאים השונים: היכן טמון הקושי בהוראת הבחנה זו לתלמידים בתיכון? את המשמעות של אינטגרל לא מסוים כפונקציה קדומה ניתן להסביר בצורה פשוטה, אך כיצד נסביר את המשמעות של אינטגרל לא מסוים במובן הפיזי שלו – כמספר ממשי? האם יש לו משמעות כזאת?
- העלו לדיון את השאלה: מה יכולים להיות היתרונות של פעילות כיתתית, בה מוצגות לתלמידים דוגמאות של שטחים מתחת לעקומות מסוגים שונים:
כאשר העקומה כולה מעל ציר ה- \(x\).
כאשר העקומה כולה מתחת לציר ה- \(x\).
כאשר חלק מהעקומה מעל הציר וחלק אחר מתחת.
כאשר ישנן שתי עקומות בווריאציות שונות ביחס לציר ה- \(x\).
יתרונות אפשריים:
– חשיפה גוברת של התלמידים לסוגי דוגמאות שונים מכינה אותם להתמודדות טובה יותר עם מקרים חדשים ולא מוכרים באותו נושא.
– פעילות מסוג זה יכולה לשמש כפעילות חקר: התלמידים יגיעו למסקנות לגבי ההשלכות של מיקום השטח מתחת לעקומה ביחס לציר ה- \(x\) על פעולת האינטגרל אותה נדרשים לבצע.
המשימה המתמטית
נתון כי הפונקציה \(g”(x)=\frac{-18}{ x^4} +\frac{18}{{x-4}^4}\) היא פונקציית הנגזרת השנייה של הפונקציה \(g(x)\).
הפונקציות \(g(x) \space,\space g'(x) \space,\space g”(x)\) מוגדרות באותו תחום.
נתון כי משוואת המשיק לפונקציה \(g(x)\) בנקודת הפיתול שלה היא \(y=\frac{3}{2}x-3\).
א. מצא את הפונקציה \(g(x)\).
ב. מהו תחום ההגדרה של הפונקציה \(g(x)\)?
ג. מצא את תחומי העלייה ואת תחומי הירידה של הפונקציה \(g(x)\).
ד. סרטט סקיצה של גרף הפונקציה \(g(x)\).
ה. נגדיר: \(h(x)=|g(x)|\). באותה מערכת צירים שבה סרטטת סקיצה של גרף הפונקציה \(g(x)\), הוסף בקו מקווקו סקיצה של גרף הפונקציה\(h(x)\).
ו. נתון כי: \(\int_{a}^{2}g(x) dx=t\) , \(0<a<2\) , \(t\) הוא פרמטר. הבע באמצעות \(t\) את \(\int_{a}^{2}(h(x)-g(x))dx\).


