בניית עזר “לא חוקית”
תיאור האירוע
התלמידים מבקשים להביא את המשימה שקיבלו לשיעורי הבית למליאה, כדי לפתור יחד עם המורה.
המורה: אוקיי, יש מי שהצליח לפתור ורוצה לבוא להראות לנו על הלוח?
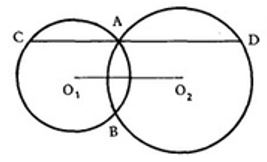
אוריין [ניגשת ללוח, משרטטת את השאלה]: האמת שזה ממש פשוט ויפה. אני עושה בניית עזר – מחברת ישר דרך הנקודות \(B\) ו-\(C\), שעובר דרך הנקודה \(O_1\). בצד השני אני מחברת ישר דרך הנקודות \(B\) ו – \(D\) שעובר דרך הנקודה \(O_2\) ונוצר לי משולש BCD.
במשולש הזה \(BO_1=CO_1=R_1\), כי כל אחד מהקטעים הללו הוא רדיוס המעגל השמאלי. בנוסף, \(BO_2=DO_2=R_2\), כי כל אחד מהקטעים הללו הוא רדיוס המעגל הימני. מכאן ש\(O_1 O_2\) הוא קטע אמצעים במשולש \(BCD\), מכיוון שקטע במשולש המחבר אמצע שתי צלעות הוא קטע אמצעים. ידוע שקטע אמצעים שווה למחצית הצלע השלישית כלומר – \(O_1 O_2=\frac{1}{2}CD\) וזה בדיוק מה שהיינו צריכים להוכיח.
המורה: תודה רבה, אוריין. (לכיתה) מה אתם אומרים? האם הפתרון של אוריין ברור? האם יש שאלות?
התלמידים: כן ברור, באמת פתרון יפה. איך לא חשבנו על זה…
המורה: תודה רבה אוריין על השיתוף, רעיון יצירתי ויפה, מיד נדבר עליו. את יכולה לחזור לשבת. האם בניית העזר כאן היא לגיטימית?
רותם: כן, בטח.
גיא: העברנו שני ישרים, כל ישר עובר מנקודה אחת על המעגל לנקודה שנייה על אותו מעגל, דרך מרכז המעגל.
יהלי: נכון, וזה מותר בהחלט!
המורה: הפתרון מתבסס על בניית עזר של המשולש \(BCD\). בחיבור הנקודה \(B\) עם הנקודה \(C\) נוצרת הצלע \(BC\). האם הצלע הזו עוברת בהכרח דרך הנקודה \(O_1\)? אולי לא? אותו דבר לגבי הצלע \(BD\), מהחיבור של הנקודות \(B\) ו- \(D\). האם הצלע עוברת בהכרח דרך הנקודה \(O_2\)? שימו לב, דרך שתי נקודות עובר רק ישר אחד, אבל דרך שלוש נקודות, לא בהכרח.
יוסי: אבל המורה, רואים בבירור בסרטוט שכל שלוש הנקודות \(B,C,O_1\) נמצאות על אותו הישר.
המורה: האם ניתן להסתמך על סרטוט כשפותרים בעיה בגאומטריה?
יוסי: אוי, נכון, באמת דיברנו על זה שאי אפשר.
תהל: אז איך נדע מתי אפשר להעביר בניית עזר ומתי לא?
המורה: שאלה טובה. באופן כללי אין מניעה להעביר כל בניית עזר שרוצים, ושאנחנו מאמינים שתעזור לנו בפתרון השאלה, בתנאי שלא משתמשים ביותר מאילוץ אחד. בשאלה שלנו למשל אפשר לחבר את \(BC\) ואת \(BD\), אבל אי אפשר להניח שהם בהכרח עוברים דרך הנקודות \(O_1\) ו- \(O_2\). אפשר לשער שזה נכון, אך צריך להוכיח זאת.
המורה עוצר, מסתכל על הלוח, וחושב רגע.
המורה: ייתכן בהחלט שבמקרה של השאלה הזו אכן הצלעות \(BC\) ו –\(BD\) עוברות דרך מרכזי המעגלים, אבל זה משהו שדורש הוכחה, והוא בהחלט לא חלק מבניית העזר שניתן להסתמך עליו. ברור לכם מה הבעיה בפתרון הזה?
תלמידים: כן. אז איך פותרים?
המורה: אוריין, תודה על השיתוף. הרעיון שלך יצירתי ויפה, אבל אי אפשר להסתמך על בניית העזר ולטעון ששלוש נקודות נמצאות בהכרח על הישר. יש עוד מישהו שרוצה לגשת ללוח ולשתף בפתרון שלו?
אוריין מציעה לפתור את הבעיה באמצעות בניית עזר לא “חוקית”. היא מניחה שהמיתר מ- \(B\) ל- \(C\) עובר בהכרח דרך מרכז המעגל \(O_1\), ובאופן דומה שהמיתר מ-\(B\) ל- \(D\) עובר בהכרח דרך מרכז המעגל \(O_2\).
- ויזואליציה מטעה: לפי הסרטוט, כמו שציין התלמיד יוסי, נראה כי מיתר העובר דרך נקודה \(B\) לנקודה \(D\) אכן עובר במרכז המעגל.
- אתגרים בבניית עזר כדרך פתרון: השימוש בבניית עזר כפתרון מצריך התייחסות למס’ גורמים במקביל:
- יש לבחור בבניית עזר מועילה, כזו שתורמת מידע רלוונטי לפתרון.
- בניית העזר יכולה לקבוע רק אילוץ אחד, מבלי להניח מעבר לאילוץ זה מידע נוסף שאינו ודאי.
- כאשר משתמשים בבניית העזר עבור שני אילוצים, יש להוכיח את נכונות הבנייה.
כך, כחלק מהתהליך בו התלמידים רוכשים את היכולת לברור את בניות העזר שמתאימות למשימה, הם אינם שמים לב לממדים אחרים, כמו החוקיות של הבניה.
- המורה מפנה לכיתה שאלות מנחות נוגעות לפתרון של אוריין. הוא שואל: מה אתם אומרים? הפתרון ברור? יש שאלות? כשהוא מקבל הסכמה מצד התלמידים על הפתרון הוא חוזר ושואל והפעם ביתר הכוונה – האם הבנייה לגיטימית, ורק לבסוף, לאחר שלא קיבל שום התנגדות מצד הכיתה לדרך הפתרון הוא מתחיל בהסבר על השגיאה. המורה מצפה שהתלמידים יבחינו בשגיאה של אוריין בעצמם, ושהתשובה תגיע מהם. יש לו כוונה לעורר דיון סביב הטענה של אוריין בכיתה, במקום למסור את הידע כולו בעצמו.
- המורה מקפיד להתייחס להיבטים רגשיים של התלמידה; חשוב לו להוקיר את המאמץ שעשתה ולתקן את השגיאה מבלי לרפות את ידיה. הוא חוזר ומודה לה על השיתוף ומחזק אותה על חשיבה מקורית.
המורה יכול להמשיך לכוון את התלמידים לכיוון המבוקש מבלי לתת את הפתרון באופן מפורש. למשל:
- אפשר לבקש מתלמיד נוסף להציג פתרון שלו על הלוח ולהשוות בין שני הפתרונות (אם לא עולה הצעה אחרת מפתרונות שהתחילו בבית, אפשר לתת זמן לעבודה כיתתית, במהלכה המורה עובר ועוזר להגיע לפתרון חדש). אז אפשר לשאול מה שונה ומה דומה בין שני הפתרונות? האם שניהם זהים? האם אחד נראה נכון יותר? להשתמש בדיון כדי להוביל את התלמידים למסקנה שבניית העזר בפתרון שהוצע כוללת הנחת יתר.
כדאי לסכם את הפעילות בהסבר על מהי בניית עזר “חוקית” – שהיא כוללת תכונה אחת בלבד, שזה נכון לכלל המקרים – מיתר במעגל, גובה וחוצה זווית במצולעים וכו’. יכול להיות שבניית עזר תגרור תכונה נוספת, אך זה תלוי בנתוני הבעיה ולא בבניית העזר בעצמה. - אפשר לבקש מהתלמידים לבדוק את הבנייה של אוריין באמצעות שימוש ביישומון ה- GeoGebra:
א. שרטטו שני מעגלים מגדלים שונים החותכים זה את זה.
ב. חברו את מרכזי שני המעגלים
ג. מתחו ישר מקביל לקטע המחבר את מרכזי המעגלים כך שהקטע מתחיל בהיקף המעגל הראשון, עובר בנקודת חיתוך שני המעגלים ומגיע אל היקף המעגל השני.
המחשת הבנייה ביישומון מאפשרת לנו להראות שהמיתרים עוברים במרכז המעגל ואחריה נוכיח את הבניה של אוריין. פעילות כזאת יכולה לזמן דיון על מה מותר להניח ואלו הנחות דורשות הוכחה. - אחרי שהמורה מודה לאוריין הוא יכול לרמוז לתלמידים בכיתה שיש בעיה עם ההוכחה של אוריין ולבקש מהם לחפש אותה. הרעיון הוא להשאיר את החיפוש פתוח ולאפשר לתלמידים לגלות בעצמם את השגיאה. לאחר מכן כדאי לתת לתלמידים להסביר את השגיאה של אוריין ולהסביר כיצד מצאו את השגיאה. בנוסף, כדאי לדון באסטרטגיות שונות לביצוע בקרה על פתרון, בתקווה שיעלו מהתלמידים. למשל, לעבור שורה שורה בפתרון ולחפש הנחות נסתרות, לפתור מחדש וכו’.
אפשר להעביר את המורים או הסטודנטים להוראה את אותו מהלך שהתרחש בכיתה כדי לדבר על הוראה של בניות עזר ולבנות אסטרטגיות הוראה שמעודדות דיון שבו עולים רעיונות שונים, או טענות ונימוקים להוכחות שלהם.
- תנו ללומדים לפתור את המשימה המתמטית, לפני הצגת כל האירוע.
- הציגו את הפתרון של אוריין ושאלו אותם מה דעתם. אם לא מתעורר דיון על נכונות בניית העזר אפשר לשאול איך פתרו, ולהשוות בין הפתרונות או לבקש מהם למצוא את מקור השגיאה בהוכחה של אוריין.
- העלו לדיון חלופות בדרכי ההוראה כדי להעמיק את הידע של התלמידים בנושא בניות עזר מועילות בגיאומטריה.
אפשר להציג ללומדים ממשימות של פרויקט משימטיקה (מכון ויצמן חומר עזר למורה) לדוגמה: בניית עזר פרופורציה ודמיון, בניית עזר במעגל. - שאלו את הלומדים: מה המקום של בניות עזר בתכנית הלימודים? מה לדעתם מרוויחים תלמידים מלמידה של בניות עזר? למשל, במקרה זה, עימות התלמידים עם הופעה של הנחה סמויה מיותרת בדרך הפתרון. עוד על הוראה ולמידה של בניות עזר בקישורים הבאים:
– קמפוס IL (בקישור)
– יחידות ללמידה עצמית (קישור)
הציעו את האפשרות ללמד את הנושא של בניות גיאומטריות דרך משחק ופתחו את נושא המשחק בשיעור לדיון: איך יראה שיעור כזה? מה היתרונות ומה החסרונות בשיעור כזה? מה יהיו המרכיבים של השיעור מעבר למרכיב המשחקי?
דוגמאות לשימוש במשחקים להוראת הנושא בניות גיאומטריות מתוך הרשת:
– Euclid the game (הסבר על המשחק אפשר למצוא כאן)
– Pythagorea (משחק לטלפון נייד, נמצא בחנויות היישומונים).
- בקשו מהלומדים לקרוא את המאמרים המצורפים לשם חקירת הנושא של בניות גיאומטריות. חומרים אלה ישמשו בסיס לדיון שתפתחו במהלך המפגש. התייחסו גם למתואר באירוע ושלבו אותו בדיון זה.
המשימה המתמטית
שני מעגלים שמרכזיהם \(O_1\) ו- \(O_2\) נחתכים בנקודות A ו- B.
נתון: \(O_1 O_2∥CD\).
הוכח: \(O_1 O_2=\frac{1}{2}CD\).