הבעה באמצעות פרמטר – פתרונות שקולים
תיאור האירוע
היכרות ראשונה עם נושא הפרמטרים בטריגונומטריה.
התלמידים עובדים על המשימה בקבוצות ולאחר מכן דנים במליאה.
במהלך התרגול מספר תלמידים פתרו את המשימה כל אחד בדרך שונה והגיעו לתשובות שונות. התלמידים מציגים דרכי פתרונות שונות, שאף אחת מהן לא מופיעה כמו בספר:
\(S_{ABCD}=\frac{a^2}{2}\cdot(\frac{1+2sin^2{\alpha}}{sin2α})\)
המורה מבקש מדן ושני (לשניהם דרכים שונות בפתרון) להציג את הפתרונות שלהם על הלוח.
דן:
\(\triangle{ADC}\)
\(tan{\alpha}=\frac{DC}{a} \Longrightarrow DC=a\cdot{tan{\alpha}}\)
נעביר גובה \(BK\) מהקודקוד \(B\) לצלע \(DC\) ונשלים את הזוויות בסרטוט, בהתאם לשוויון בין הצלעות \(AB\) ו \(BC\) ולפי השוויון בין הזוויות המתחלפות \(\measuredangle{BAC}\) ו \(\measuredangle{ACD}\):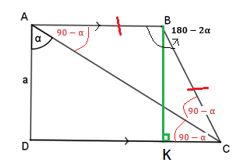
נתון \(AD=BK=a\), לכן:
\(\triangle{BKC}\)
\(sin (180-2\alpha)=\frac{a}{BC}\Longrightarrow BC=\frac{a}{sin (180-2\alpha)}\)
נתון: \(AB=BC\)
לכן \(AB=\frac{a}{sin (180-2\alpha)}\)
\(S_{ABCD}=\frac{(AB+DC)\cdot AD}{2}\)
\(S_{ABCD}=\frac{(\frac{a}{sin (180-2\alpha)}+a\cdot tan\alpha)\cdot a}{2}\)
שני:
\(\triangle{ADC}\)
\(tan \alpha=\frac{DC}{a} \Longrightarrow DC=a\cdot tan \alpha\)
\(\frac{a}{AC}=cos \alpha \Longrightarrow AC=\frac{a}{cos \alpha}\)
משפט הסינוסים במשולש \(\triangle{ABC}\)
\(\frac{AB}{sin(90- \alpha)}=\frac{AC}{sin2 \alpha} \Longrightarrow AB=\frac{\frac{a}{cos \alpha} \cdot sin(90- \alpha)}{sin2 \alpha}\)
\( \Longrightarrow AB=\frac{a \cdot sin(90- \alpha)}{cos \alpha \cdot sin2 \alpha}\)
\(S_{ABCD}=\frac{(AB+DC)\cdot AD}{2}\)
\(S_{ABCD}=\frac{(\frac{a\cdot sin(90-\alpha)}{cos \alpha \cdot sin2 \alpha)}+a\cdot tan\alpha)\cdot a}{2}\)
התלמידים שמים לב שהתשובות שונות זו מזו, ומזו שבספר.
דן: איך זה שכל אחד מאתנו קיבל פתרון שונה? המתמטיקה לא הגיונית!
המורה בודק ומוצא את שני הפתרונות נכונים. הוא מתכוון להראות לתלמידים איך שתי התשובות זהות באמצעות שימוש ב”זהויות”, שהתלמידים מכירים, אבל לא מספיק מפאת קוצר הזמן.
המורה: בדרך של הוכחה על ידי שימוש בזהויות ניתן להראות שבעצם הפתרונות שלכם שקולים זה לזה. אני מזמין אתכם לנסות להוכיח בבית את מה שלא הספקנו בשיעור.
התלמידים רגילים שלכל משימה מתמטית מתקיים פתרון יחיד, שהוא הפתרון שמופיע בספר. המצב שבו תלמידים שונים מקבלים פתרונות שונים, שלא מופיעים בספר, מבלבל אותם. (כמו שדן אומר “המתמטיקה לא הגיונית”). סביר להניח שאם המורה היה מספיק להוכיח איתם שקילות של שני פתרונות לפחות, הוכחה כזאת הייתה מרגיעה אותם ומניחה את דעתם.
המורה לא צפה מצב שבו יתקבלו פתרונות שונים מצד התלמידים, ושהוא יצטרך להסביר איך אפשר להגיע לכל פתרון בעזרת זהויות. ההחלטה להראות הוכחה תוך שימוש בזהויות לשקילות הפתרונות, היא החלטה שקיבל באותו רגע, משחווה את התסכול של התלמידים. הוא רצה להתייחס לכך בשיעור, אך כיוון שלא הכין אותה מראש לא הספיק לעשות זאת בצורה מסודרת.
- הצבת מספרים: על מנת לתת מענה מידי לתלמידים בזמן הקצר שנשאר עד לסוף השיעור, ניתן לרשום על הלוח שני פתרונות שונים שקבלו תלמידים, ואז לשאול כיצד לדעתם ניתן להוכיח שהפתרונות שקולים? השאיפה היא שהתלמידים יציעו להציב ערכים זהים עבור הצלע הנתונה והזווית הנתונה בשני הפתרונות, כך שתתקבל תוצאה מספרית זהה (אם הרעיון לא יגיע מצד התלמידים המורה יכוון אותם).
*כדי לוודא שהתוצאה המספרית הזהה לא התקבלה במקרה יש לבצע 2-3 הצבות שונות.
לשיטה זו שני יתרונות עיקריים:
– זו שיטה מהירה ופשוטה לביצוע, וניתן לבדוק על ידה האם הפתרונות זהים עבור הערכים שהוצבו, ואז יש סיכוי כי הם אכן שקולים.
– על דרך זו אפשר להחזיר לתלמידים את הבטחון ב”שלמות המתמטיקה”; התלמידים יראו שעל אף שיכולות להתקיים דרכים שונות לפתרון, ותשובות שלמראית עין נראות שונות’ כאשר יציבו מספר אחיד בשני פתרונות יראו שהפתרונות זהים (חשוב לוודא את נכונות דרכי הפתרון לפני שמשווים בין הפתרונות).
החיסרון בשיטה זו, הוא שהצבה זו אינה מהווה הוכחה מתמטית לשקילות הפתרונות. על מנת להוכיח שקילות יש להשתמש בכלים מתמטיים (כמו שימוש בזהויות), אשר יוכיחו שקילות עבור הפרמטר כאובייקט כללי, ולא עבור מספר כזה או אחר.
חיסרון נוסף הוא שהצבה אחת לא מספיקה, כי אפשר לטעון שהזהות המספרית התקבלה במקרה או בגלל טעות הקלדה. (אך התלמידים לא נדרשים להוכחה כזאת, אלא רק לצורך השוואת הפתרונות כדי לוודא שפתרו נכון). - להדגים את העיקרון בעזרת תרגילים דומים ופשוטים.
נסתכל, למשל, על משולש ישר זווית שבו נתונה זווית \(\alpha\) וניצב מולה \(a\) ויש לחשב את היתר \(c\). מקרה זה, אפשר לחשב בשני אופנים:
\(c=\frac{a}{sin \alpha}\) או \(c=\frac{a}{cos (90- \alpha)}\)
בבחירת דרך הפתרון (במקרה זה בחירת הזווית שנעבוד איתה) אנחנו משפיעים על הצורה של התשובה הסופית, אך לא על ערכה (אפשר להציב מספרים שווים בשני הביטויים כדי לבדוק זאת).
משימה להגשה בהקשר האירוע:
- קראו את תיאור האירוע.
- סמנו את הרגע הקריטי בשיעור וכתבו מדוע לדעתכם הוא קריטי.
- נסו להיזכר באירוע דומה משיעור בו לימדתם או צפיתם (תוכלו לקחת אירוע מתוך צפייה בשיעורים בפרויקט עדש”ה או ממקור אחר). תארו אותו בפירוט מלא בכתב: מה היה הרקע לאירוע, מהלך האירוע, כיצד הגיב.ה המורה למתרחש בכיתה, דעתכם על התגובה, וכיצד אתם הייתם פועלים במקומו?
- קראו את האסטרטגיות המוצעות באירוע זה ובחרו אסטרטגיה אחת המועדפת עליכם. כתבו מדוע הייתם בוחרים להשתמש בה.
- כתבו אסטרטגית הוראה חלופית נוספת לאסטרטגיות המוצעות כאן, שמטרתה להתמודד עם שקילות הפתרונות בהבעה באמצעות פרמטר בטריגונומטריה. כתבו את היתרונות והחסרונות לשימוש בה.
המשימה המתמטית
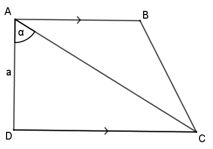
בטרפז ישר זווית \(ABCD\space\) \((AB||CD\space,\space \measuredangle{ADC}=90^{\circ}) \)
נתון: \(AB=BC \space,\space AD=a \space,\space \measuredangle{DAC}=\alpha\)
הבע בעזרת \(a\) ו- \(\alpha\) את שטח הטרפז.