פתרון בעיות קיצון בגרפים באמצעות תכונות של סימטריה
תיאור האירוע
התלמידים עובדים בזוגות על המשימה.
המורה מזהה בקרב חלק מהתלמידים התלבטות לגבי המשך פתרון המשימה. הוא מרכז את כולם במליאה, כדי שיציגו פתרונות שלהם, או תהיות לגבי הפתרון.
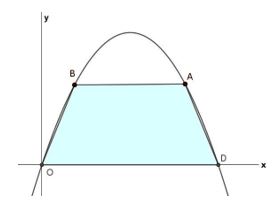
שיר ושני: בשביל לחשב את שטח הטרפז צריך לכפול את חצי הגובה בטרפז בסכום הבסיסים. צריך למצוא את שיעורי הנקודות A ו-B, כדי למצוא את האורך של הבסיסים.
השתמשנו בפרמטר \(t\), כדי להביע את שיעורי הנקודה A כך: \((t,6t-t^2)\)A.
לגבי B, אנחנו מסכימות, שערך ה-\(y\) של הנקודה זהה לזה של הנקודה A. לגבי הערך \(x\) של הנקודה – אנחנו מתלבטות.
שי ומרים: אפשר להשתמש בתכונות הסימטריה של הפרבולה.
זוהר: הטרפז החסום בתוך הפרבולה הוא שווה שוקיים ומורכב משני משולשים חופפים ומלבן. אפשר “לגזור” את המשולש הימני, לסובב ולהדביק אותו ליד המשולש השמאלי כדי לקבל מלבן. אז קדקוד A של המלבן יהיה על גרף הפונקציה בחלק שבו היא יורדת, וקדקוד O נמצא בראשית הצירים.
שיעור קדקוד A הוא \((x,6x-x^2)\)A. ופונקציית המטרה היא שטח המלבן, כלומר \(y=x(6x-x^2)\).
כך ממשיכה זוהר בפתרון על ידי שימוש בנגזרת.
המורה: יפה! איזו תשובה מקורית! את יכולה להסביר את הפתרון? ואיך חשבת על זה?
זוהר מוצאת כי הטרפז החסום הוא שווה שוקיים.
1. ויזואליזציה שמקדמת: היא עושה זאת כי היא מסתמכת על הסרטוט.
2. היא מסתמכת על תכונת הסימטריה של פרבולה ביחס לציר הסימטריה שלה, בעקבות ההצעה של שי ומרים, ומכאן מסיקה על הסימטריה של הטרפז. מתוך ההיכרות עם טרפז שווה שוקיים, היא יוצרת מלבן שווה שטח לשטח הטרפז כדי לפתור את השאלה ביתר קלות.
- המורה מקבל את ההצעה המקורית של זוהר כהפתעה. הוא מבקש ממנה להציג את הפתרון שלה בפני כל הכיתה, כדי לבסס עבור התלמידים את הכיתה כמרחב לימודי שבו יש פתיחות לרעיונות חדשים.
- המורה מבקש מזוהר להציג את הפתרון שלה בעצמה. כאשר הוא בוחר לעשות זאת, במקום להציג אותו בעצמו, הוא מתכוון להעצים את התלמידה ולעודד אותה על חשיבה מקורית – לשקף לה ולאחרים שיש מקום לנסות לפתור שאלות בדרכים שונות.
- אפשר לבקש מהתלמידה להסביר מדוע לדעתה הטרפז שווה שוקיים.
כשמורה מבקש מתלמיד.ה להסביר טענותיו.ה, הוא מזכיר לתלמידים שחשוב לצרף הסבר ו/או הוכחה מתאימים לכל טענה שמעלים במהלך הפתרון.
עצם הנימוק, מאלץ את התלמידה לחזור ולנסח ביתר דיוק את טענתה בהתבסס על תכונת הסימטריה של הפרבולה, ובתוך כך להעמיק את ההבנה שלה ושל האחרים בנושא. - אפשר לבקש משאר התלמידים לנסות למצוא דרכים נוספות לפתרון. למשל, הם יכולים לנסות להמשיך את קו המחשבה של שי ומרים בפתרון – להביע את שיעורי הנקודות A ו-B בהתבסס על תכונות הסימטריה של הפרבולה. או בדרך האלגברית: להביע את שיעור ה- \(x \) של נקודה B, תוך שימוש בפרמטר \( t\), באמצעות הנוסחה להפרש ריבועים, או באמצעות השלמה לריבוע (ראו קובץ ‘פתרונות נוספים למשימה המתמטית’ תחת הקישור לאירוע). בדרך זו, התלמידים משכללים מיומנות של פתרון בדרכים שונות וגם מעשירים את הידע המתמטי שלהם. למידה שבה לא מסתפקים רק בדרך אחת לפתרון היא למידה חווייתית ומשמעותית יותר.
3. אפשר לבקש מהתלמידים להביא הצעות (מהספר או מעצמם) לשאלות דומות שניתן לפתור אותן בדרך של זוהר – לחתור לשטח פשוט יותר לחישוב דרך “גזירה”. בדרך זו, התלמידים משתתפים בפעילות חקר מדרגת חשיבה גבוהה ומחזקים יכולות של למידה עצמית.
1. בקשו מהלומדים לפעול לפי אסטרטגיות הוראה חלופיות שפורטו בסעיף הקודם:
– לפתור את השאלה בדרכים נוספות.
– לנמק את נכונות הפתרון של התלמידה.
– למצוא או לחבר משימות דומות לפתרון בדרך דומה של גזירת צורה והדבקה.
2. בקשו מהלומדים להביא דוגמאות משלהם לאירוע בו תלמיד פתר שאלה בנושא מתמטי מסוים על ידי פתרון הלקוח מנושא מתמטי אחר. דונו מה דומה ומה שונה בין האירועים.
המשימה המתמטית
בתוך פרבולה שמשוואתה \(y=6x-x^2\) חוסמים טרפז ABOD כמתואר בסרטוט.
מכל הטרפזים השונים שניתן לחסום באופן הזה, מצא את שטחו של הטרפז בעל השטח המקסימלי.